[Q1] 바닥 면적이 같지만 모양이 다른 두 용기에 같은 양의 물을 채워 넣었다. 비어있는 두 용기의 무게는 같다. 바닥이 받는 수압이 더 큰 쪽은?
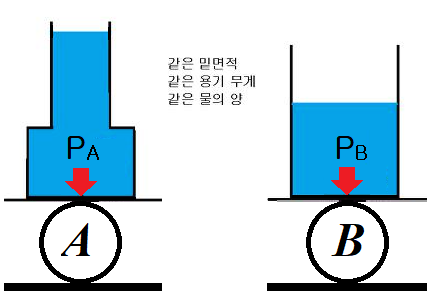
깊이에 따른 수압은 $P=P_{0} + \rho g h$이므로, 수면으로부터 더 깊은 바닥(A)에 더 큰 수압이 작용한다. 그런데 바닥의 면적이 같다고 했으므로 수압이 용기 바닥에 주는 힘은 A가 더 커야 한다.
[Q2] 이제 두 용기를 저울에 올려보자. 저울 눈금이 더 크게 나오는 것은? 수압이 바닥에 주는 힘은 A가 더 큰 데, 용기+물의 무게는 두 경우 모두 같다. 눈금이 더 큰 쪽은 A일까? 아니면 B? 그도 아니면 같을까?
'Physics > 유체역학' 카테고리의 다른 글
| 유체 기둥이 잘못된 것은? (1) | 2016.01.27 |
|---|---|
| 무엇이 잘못 되었을까? (0) | 2016.01.26 |
| 저울의 눈금은 어떻게 변할까? (1) | 2016.01.25 |
| 떨어지는 물병에 뚫린 구멍에서 물이 샐 수 있나? (0) | 2016.01.24 |
| 모래가 섞인 얼음이 녹을 때 수면의 높이는? (0) | 2016.01.19 |






