주변에 보이는 많은 선 중에는 직선도 있고 휘어진 곡선도 있다. 그럼 수학적으로 곡선이 휘어진 정도를 어떻게 정의할까? 곡선의 각각의 부분에서 휘어진 정도가 다 다르므로, 휘어진 정도는 곡선의 위치에 따라 달라지는 값이 될 것이다. 평면에 놓인 곡선의 기술할 때 보통은 $x, y$ 좌표를 많이 사용하는데, $x$ 방향으로 움직이면서 $y$의 값이 변하는 정도를 재는 것으로 곡선의 휘어짐을 정의할 수 있지 않을까? 직선을 살펴보면 $x$ 축으로 움직이면 $y$의 값이 변하는데, 통상 직선은 휘어져 있다고 이야기하지 않으므로, 이러한 방법은 휘어짐을 정의하기에는 적당하지 않다. 곡선 위의 임의 지점에서 곡선의 휘어짐은 그 지점에서 접선 방향으로 움직였을 때, 접점에서 많이 벗어날 수로 접선과의 차이가 크면 곡선은 많이 휘어졌다는 것은 직관적으로 알 수 있다. 이것을 좀 더 수학적으로 이야기하면 곡선을 따라가면 접선의 방향이 얼마나 변했는가를 재면 곡선이 휘어진 정도를 알 수 있다는 것을 의미한다. 그런데 곡선을 따라갈 때 빨리 갈 수도 또는 느리게 갈 수도 있으므로, 곡선을 따라가는 비율을 고정해야 한다. 가장 간단한 방법은 곡선을 따라 움직이는 거리를 기준으로 접선의 변화가 얼마나 생기는 가를 재면 된다. 곡선의 길이($s$)를 매개변수로 사용하면 곡선 위의 임의 지점에서 접선 벡터는 크기는 항상 1로 주어진다:
$$ds^2=dx^2 + dy^2 \quad \rightarrow\quad \sqrt{ \Big(\frac{dx}{ds}\Big)^2 + \Big(\frac{dy}{ds}\Big)^2 } = 1.$$
곡선의 휘어짐은 곡률이라는 용어를 사용하는데, 엄밀하게 정의하면 곡선의 한 지점에서 곡률은 그 지점에서 접선 벡터
$$\vec{T} = \left(\frac{dx}{ds},\frac{dy}{ds} \right)$$
의 미분계수의 크기로 주어진다:
$$\kappa = \Big| \frac{d\vec{T}}{ds}\Big| = \sqrt{\Big(\frac{d^2x}{ds^2} \Big)^2 + \Big(\frac{d^2 y }{ds^2} \Big)^2 }.$$
접선 벡터 $\vec{T}$는 길이가 1이므로 미분한 값은 $\vec{T}$에 수직하고, 곡선이 안쪽으로 휘어지는 쪽을 가리킨다. $\vec{T}$에 수직인 방향의 단위 벡터를 $\vec{N}$이라 하면(보통 $\vec{T}$에서 반시계 방향으로 회전된 방향, $\vec{T}\cdot \vec{N}=0$) $d\vec{T}/ds$는 $\vec{N}$에 비례하고 비례항의 크기가 그 지점에서 곡률이다.
$$\frac{d\vec{T}}{ds} =k \vec{N},\quad \kappa = |k|. $$
즉, 곡률이 클수록 같은 길이를 옮겨갈 때 $T$의 방향 변화가 심하게 일어난다. 주어진 $T$방향에 대해서 곡선이 휘어지는 방향이 오른쪽이나 왼쪽이 될 수 있으므로 $k$는 부호를 가지게 된다. 반지름이 $R$인 원이 있다고 하자(중심=원점, $(R,0)$에서 거리를 재면),
$$x(s)=R \cos(\theta)=R\cos (s/R)$$
$$ y(s) = R \sin (\theta)=R \sin (s/R)$$
$$ \therefore \kappa =\frac{1}{R}$$
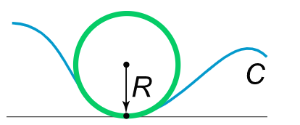
이므로 곡률은 반지름의 역수로 주어진다. 반지름이 작을수록 같은 거리를 움직일 때 접선의 방향 변화가 심하므로 곡률이 더 크게 나타날 것이라는 것은 쉽게 예상할 수 있다. 직선의 경우에는 접선 벡터가 일정하므로 곡률은 당연히 0이다.
일반적인 매개변수($t$)인 경우
$$\vec{T} = \left(\frac{dx}{ds},\frac{dy}{ds} \right) = \frac{1}{\dot{s}} ( \dot{x}, \dot{y} ) = \frac{1}{\sqrt{\dot{x}^2 + \dot{y}^2 }} (\dot{x}, \dot{y})$$ 이므로 (overdot은 매개변수 $t$-에 대한 미분)
$$\kappa = \frac{|\dot{x}\ddot{y} - \dot{y} \ddot{x}|}{( \dot{x}^2 + \dot{y}^2 )^{3/2}}.$$
하나의 예로 catenary의 경우를 계산해 보자. 매개변수로 표현된 catenary 곡선은
$$ x(t) = a \sinh^{-1}(t),\quad y(t) = a\sqrt{1+t^2}\quad (y=a\cosh(x/a))$$
이고, $a$는 장력의 수평성분을 줄의 선밀도와 중력가속도의 곱으로 나눈 양이다. $a$가 증가할수록 줄이 평평해지려는 경향이 있으므로 곡률이 전반적으로 줄어들 것으로 예상할 수 있다. 실제로 곡률을 계산하면
$$ \kappa = \frac{1}{a(1+t^2)}=\frac{a}{y^2}$$
임을 알 수 있다.
'Computational Geometry' 카테고리의 다른 글
| Monotone Cubic Interpolation (0) | 2012.09.09 |
|---|---|
| Brute Force Convex Hull Algorithm (0) | 2012.09.06 |
| Douglas-Peucker Algorithm (0) | 2012.05.03 |
| Inside Quadrilateral, Inside Triangle (0) | 2012.01.18 |
| 3개의 숫자 중에서 가장 큰 것은 (0) | 2012.01.17 |




