3차의 Hermite spline을 쓰는 interpolation에서 입력 데이터 점에서의 기울기 값을 수정하면 입력 데이터의 monotonic 한 성질을 그대로 유지하는 보간을 할 수 있다. 주어진 데이터가 $\{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\}$이고, $x/y$-좌표가 증가하는 순으로 정렬되었다고 하자. 구간 $[x_k, x_{k+1} ]$의 시작과 끝에서 값 ($p_0 = y_k $, $p_1=y_{k+1}$)과 기울기 ($m_0, m_1$) 가 주어지면 cubic Hermite spline 보간 함수는 다음과 같이 매개변수 $t \in [0,1]$의 함수로 표현된다:
$$f(t) = p_0 h_{00}(t) + m_1 h_{10}(t) + p_1 h_{01}(t) + m_1 h_{11}(t), \quad \quad t= \frac {x-x_k}{x_{k+1}-x_k} $$
$$f(0) = p_0,\quad f'(0) = m_0,\quad f(1) = p_1,\quad f'(1)=m_1$$
Hermite 기저 함수의 정의는 아래와 같다:
$$ h_{00}(t) = 2t^3 - 3t^2+1$$
$$ h_{10}(t) = t^3 - 2t^2+t$$
$$ h_{01}(t)=-2t^3+3t^2$$
$$ h_{11}(t)=t^3-t^2$$
이를 보이기 위해 3차 보간함수를
$$f(t) = a_0 + a_1t+a_2t^2 + a_3 t^3,\qquad 0 \le t \le 1$$으로 놓고, constraints를 부여하면
\begin{align} p_0 &= f(0) = a_0 \\ p_1 &= f(1) = a_0+a_1+a_2+a_3 \\ m_0 &= f'(0) = a_1 \\ m_1 &= f'(1) = a_1 + 2a_2 + 3a_3 \end{align}을 얻을 수 있다. 계수 $a_0, a_1, a_2, a_3$에 대해 풀면
$$ f(t) = p_0 + m_0 t + (3p_1 - 3p_0 -m_1 -2 m_0) t^2 + (-2p_1 +2p_0 + m_0 + m_1 )t^3$$
$$ = p_0 (2t^3-3 t^2 +1) + p_1 ( -2 t^3 + 3t^2) + m_0 ( t^3 - 2t^2 +t) + m_1 ( t^3- t^2)$$ 처럼 표현됨을 알 수 있다.
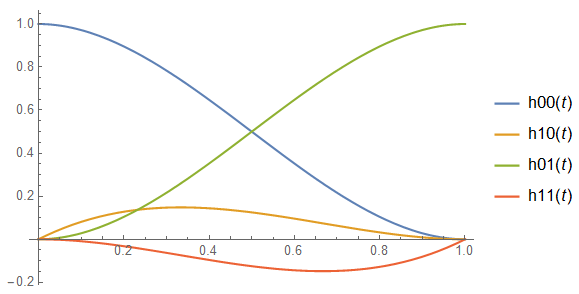
보간 spline이 단조성(monotonicity)을 가지도록 하려면 각 입력점에서 기울기 값($m_{k}$)을 조절해주어야 하는데, 기울기 $m_{k}$를 어떻게 설정해야 인접 구간의 보간 함수와 smooth 하게 연결될 수 있을까? 주어진 입력점에서 기울기는 보통 왼쪽과 오른쪽 인접 입력점에서 각각 평균 변화율($\delta_{k-1}, \delta_{k}$)을 구한 후 이들의 평균을 사용하면 된다. (양 끝점에서는 오른쪽이나 왼쪽 구간의 평균 변화율로 대체)
$$ m_k = \frac {1}{2}(\delta_{k-1}+\delta_{k} )= \frac {1}{2}\left(\frac { y_k-y_{k-1}}{x_k - x_{k-1}}+\frac {y_{k+1}-y_k}{x_{k+1} + x_k}\right)$$
이것만으로는 단조성을 보증을 할 수 없으므로 다음 조건을 추가로 부여해야 됨이 관련 논문에서 증명이 되었다.
$$1.~ \text{For}~~\delta_{k} = 0 \quad\Longrightarrow\quad m_k =m_{k+1} = 0$$
$$2. ~\text{For}~~\epsilon=\sqrt {\left(\frac {m_k }{\delta_k }\right)^2 + \left(\frac {m_{k+1}}{\delta_{k} }\right)^2 } > 3$$
$$ \quad\Longrightarrow\quad m_{k} \leftarrow3\frac {m_{k}}{\epsilon}, ~m_{k+1} \leftarrow 3\frac {m_{k+1}}{\epsilon}$$
아래의 코드는 위키피디아에 제시된 알고리즘을 구현한 것이다. (입력 데이터가 한 방향으로 monotonic 할 때만 동작함)
참고: http://en.wikipedia.org/wiki/Monotone_cubic_interpolation
std::vector<double> estimateTangents(const std::vector<CfPt>& P) {
// slopes;
std::vector<double> delta(P.size());
for (int k = 0; k < delta.size()-1; k++)
delta[k] = double(P[k+1].y - P[k].y) / (P[k+1].x - P[k].x) ;
// average tangent at data points;
std::vector<double> m(P.size());
m.front() = delta.front();
m.back() = delta[m.size()-2];
for (int k = 1; k < m.size()-1; k++)
m[k] = (delta[k-1] + delta[k]) / 2; //error corrected.
for (int k = 0; k < m.size()-1; k++) {
if (delta[k] == 0) m[k] = m[k+1] = 0;
else {
double alpha = m[k] / delta[k];
double beta = m[k+1] / delta[k];
double epsilon = hypot(alpha, beta);
if (epsilon > 3) {
double tau = 3 * delta[k] / epsilon ;
m[k] = tau * alpha;
m[k+1] = tau * beta;
}
}
}
return m;
};std::vector<CfPt> monotoneCubicSplineInterp(const std::vector<CfPt>& points) {
if (points.size() <= 2) return points;
// tangent table;
std::vector<double> m = estimateTangents(points);
// hermite spline;
#define STEPS 12
std::vector<CfPt> curve;
curve.push_back(points.front()); //add first point;
for (int i = 0; i < points.size()-1; i++) {
double h = points[i+1].x - points[i].x;
for (int k = 1; k <= STEPS; k++) {
double t = double(k) / STEPS; // 0 < t <= 1;
double tt = t*t, ttt = tt*t;
double h00 = 2 * ttt - 3 * tt + 1;
double h10 = ttt - 2 * tt + t;
double h01 = -2 * ttt + 3 * tt;
double h11 = ttt - tt;
double yf = h00 * points[i].y + h10 * h * m[i]
+ h01 * points[i+1].y + h11 * h * m[i+1];
curve.push_back(CfPt(points[i].x + t * h, yf));
}
}
return curve;
};Natural cubic spline과의 비교:
Natural Cubic Spline
구간 $[a=t_0, ...t_{n-1}=b]$에서 일정한 간격(꼭 일정한 간격일 필요는 없지만 여기서는 1로 선택함)으로 샘플링된 데이터 $\{ f_0, ...f_{n-1} \}$이 있다. $n-1$ 개의 각 구간에서 데이터를 보간하는 삼차다
kipl.tistory.com
'Computational Geometry' 카테고리의 다른 글
| Chain Hull (2) | 2012.09.16 |
|---|---|
| Quick Hull (2) | 2012.09.16 |
| Brute Force Convex Hull Algorithm (0) | 2012.09.06 |
| Curvature of a Curve (0) | 2012.08.07 |
| Douglas-Peucker Algorithm (0) | 2012.05.03 |




