Geometry & Recognition

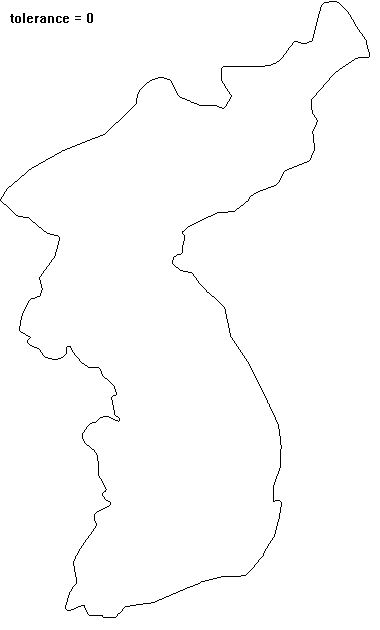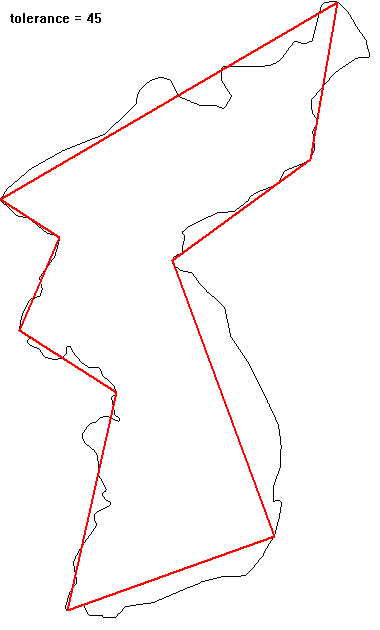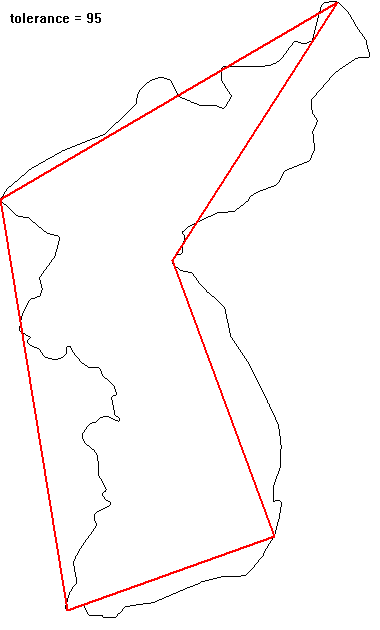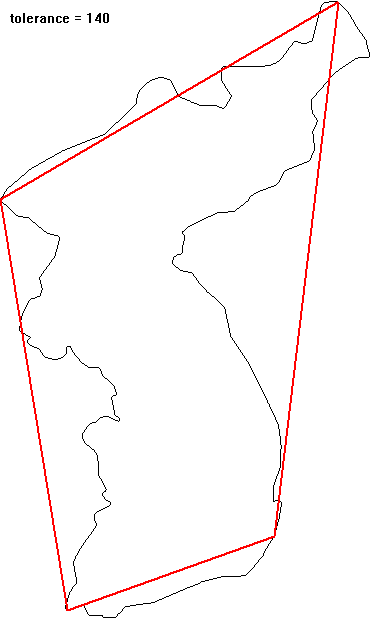
일정한 간격(예를 들면 1)으로 sampling 된 물체의 윤곽정보가 있다고 하자. 이 윤곽정보를 좀 더 적은 데이터를 이용해서 표현하려고 할 때 가장 쉬운 방법 중 하나는 샘플링 간격을 2배로 늘리는 것이다(down sampling). 이는 더 큰 스케일에서 물체를 바라보는 것과 동일한 효과를 준다. 그러나 down sampling에서 일부의 원정보가 사라지게 되므로 이에 대한 보정이 필요하게 된다. Down sampling 된 데이터에서 버려진 중간지점(홀수)의 정보는 선형적으로 예측할 수 있지만 이는 충분하지 못하다. 따라서 down sampling 할 때 버리지는 부분이 지니고 있는 고주파 성분을 저장한 후 이를 down sampling 된 저주파 성분의 보정에 사용해야 할 필요가 생긴다.

그러면 다운 샘플링과정에서 잃어버리는 고주파 성분은 어떻게 알아낼 수 있을까? 이는 다운 샘플링된 데이터로 원 데이터를 구성하려면 보간 방법을 사용하는데, 원 데이터에서 보간 값을 빼주면 근사적으로 예측할 수 있다. 다운 샘플링된 저주파 성분에 예측된 고주파 성분을 일정 부분 추가함으로써 더 정교한 다운샘플링을 할 수 있다. 이는 wavelet 변환에서 lifting-update 과정에 해당한다. 여기서는 이 알고리즘을 복잡한 폴리곤을 단순화시키는 과정에 적용해 본다. 보간 방법으로 Catmull-Rom spline을 이용했다. Douglas-Peucker 알고리즘에서는 변화지 않는 두 개의 고정점이 있지만, 이 방법에서는 모든 점이 변할 수 있다. 알고리즘을 반복 적용하면 매회 1/2로 다운샘플링되므로 어느 단계를 넘어서면 과도하게 단순화되는 단점이 있다. 입력점의 개수가 2의 지수승이 아닌 경우는 마지막 점을 반복해서 넣어주면 된다. 

// at t=1/2 (p0, p1, p2, p3);
CfPt catmull_rom(const CfPt& p0, const CfPt& p1, const CfPt& p2, const CfPt& p3) {
    return ((p1 + p2) * 9 - (p0 + p3)) / 16;
}
// 홀수점에서 고주파 성분을 주변 4개의 짝수점으로 만든 
// catmull-rom 스프라인을 이용해서 예측;
void lift(const std::vector<CfPt>& points,
          std::vector<CfPt>& hf_comp) {
    ASSERT(!(points.size() & 1) &&  points.size() >= 2);
    hf_comp.resize(points.size() / 2);
    for (int i = 1; i < points.size(); i += 2) {
        const int im3 = max(i-3, 0);
        const int im1 = i-1;
        const int ip1 = min(i+1, points.size()-1);
        const int ip3 = min(i+3, points.size()-1);
        // high freq comp = observed - estimated values;
        hf_comp[i/2] = points[i] - catmull_rom(points[im3], points[im1], points[ip1], points[ip3]);
    }
}
// update
// 고주파 성분 예측 에러가 필터링된 저주파 성분(짝수항)을 계산함
// 짝수항(저주파 성분)에 근방에서 구한 고주파 성분 평균의 절반을 더해줌;
void update(const std::vector<CfPt>& points,
            const std::vector<CfPt>& hf_comp,
            std::vector<CfPt>& lf_comp) {
    ASSERT(!(points.size() & 1));
    lf_comp.resize(points.size() / 2);
    for (int i = 0; i < points.size(); i += 2)
        // high[i/2]은 points 기준으로 (i+1)위치임;
        lf_comp[i/2] = points[i] + ((i==0 ? CfPt(0,0): hf_comp[i/2-1]) + hf_comp[i/2]) / 4;
}
std::vector<CfPt> decimate_polygon(const std::vector<CfPt>& points, const int max_pass) {
    const int orig_sz = points.size();
    int two_power = 1; 
    while (two_power < orig_sz) two_power <<= 1;
    // last element padding;
    std::vector<CfPt> input = points;
    const CfPt q_padd = input.back();
    for (int k = input.size(); k < two_power; k++) 
        input.push_back(q_padd);
    // wavelet passes
    std::vector<CfPt> hf_comp;
    std::vector<CfPt> lf_comp;
    // max_pass = max(max_pass-2, 0); // points.size()<= 2^max_pass;
    int pass = 0;
    while (pass++ < max_pass) {
        if (pass > 1) input.swap(lf_comp);
        lift(input, hf_comp);
        update(input, hf_comp, lf_comp);
    }   
    lf_comp.resize(orig_sz>>pass);
    return lf_comp; //decimated polyline;
};

https://kipl.tistory.com/99

영상에서 추출한 객체(object)의 경계선은 객체의 모양에 대한 많은 정보를 담고 있지만, 어떤 경우에는 불필요하게 많은 정보가 될 수도 있다. 이 경우 원래의 경계를 충분히 닮은 다각형으로 간략화하여서 불필요한 정보를 제거할 수 있다. 이 다각형으로의  근사가  물체의 경계를 얼마나 제대로 표현할 수 있는지에 대한 기준이 있어야 한다. $N$개의 점 $\{(x_i, y_i) | i = 1,... ,N\}$으로 표현된 경계가 있다고 하자. 가장 단순한 근사는 가장 멀리 떨어진 두 점($A, B$)으로 만들어진 선분일 것이다(선분의 길이가 대략적인 물체의 크기를 주고, 선분 방향이 물체의 orientation을 알려준다). 이 선분을 기준으로 다시 가장 멀리 떨어진 점($C$)을 찾아서 일정 거리 이상 떨어져 있으면 꼭짓점으로 추가하여 두 개의 선분으로 분할한다. 두 개의 선분에 대해서 동일한 분할 작업을 재귀적으로 반복하므로 좀 더 정밀하게 물체를 표현하는 다각형을 찾을 수 있다. 선분에서 가장 멀리 떨어진 지점이 기준 거리 이내이면 분할을 멈춘다. 닫힌 다각형 근사일 때는 시작점 = 끝점으로 조건을 부여하면 된다.

** open polyline으로 우리나라 경계를 단순화시키는 예: top-right 쪽이 시작과 끝이므로 simplication 과정에서 변화지 않는다.

// distance square from P to the line segment AB ;

double pt2SegDist2(CPoint P, CPoint A, CPoint B) ;

// P에서 두 점 A, B을 연결하는 선분까지 거리
double pt2SegDist2(CPoint P, CPoint A, CPoint B) {
    double dx = B.x - A.x, dy = B.y - A.y ;
    double lenAB2 = dx * dx + dy * dy ;
    double du = P.x - A.x, dv = P.y - A.y ;
    if (lenAB2 == 0.) return du * du + dv * dv;
    double dot = dx * du + dy * dv ; 
    if (dot <= 0.) return du * du + dv * dv;
    else if (dot >= lenAB2) {
        du = P.x - B.x; dv = P.y - B.y;
        return du * du + dv * dv;
    } else {
        double slash = du * dy - dv * dx ;
        return slash * slash / lenAB2;
    }
};

//  recursive Douglas-Peucker 알고리즘;

void DouglasPeucker(double tol, std::vector<CPoint>& vtx, int start, int end, 
                   std::vector<bool>& mark) {
    if (end <= start + 1) return; //종료 조건;
    // vtx[start] to vtx[end]을 잇는 선분을 기준으로 분할점을 찾음;
    int break_id = start;			// 선분에서 가장 먼 꼭짓점;
    double maxdist2 = 0;
    const double tolsq = tol * tol;		
    for (int i = start + 1; i < end; i++) {
        double dist2 = pt2SegDist2(vtx[i], vtx[start], vtx[end]);
        if (dist2 <=  maxdist2) continue;
        break_id = i;
        maxdist2 = dist2;
    } 
    if (maxdist2 > tolsq) {		// 가장 먼 꼭짓점까지 거리가 임계값을 넘으면 => 분할;
        mark[break] = true;		// vtx[break_id]를 유지;
        // vtx[break_id] 기준으로 좌/우 polyline을 분할시도;
        DouglasPeucker(tol, vtx, start, break_id, mark);
        DouglasPeucker(tol, vtx, break_id, end, mark);
    }
};

// driver routine;

std::vector<CPoint> polySimplify(const double tol, const std::vector<CPoint> &V) {
    if (V.size() <= 2) return V;    
    std::vector<bool> mark(V.size(), false); // 꼭짓점 마킹용 버퍼;
    // 알고리즘 호출 전에 너무 붙어있는 꼭짓점을 제거하면 보다 빠르게 동작;
    // 폐곡선이 아닌 경우 처음,끝은 marking; 
    // 폐곡선은 가장 멀리 떨어진 두점중 하나만 해도 충분;
    mark.front() = mark.back() = true; 
    DouglasPeucker( tol, V, 0, V.size()-1, mark );
    // save marked vertices;
    std::vector<CPoint> decimated;
    for (int i = 0; i < V.size(); i++)
        if (mark[i]) decimated.push_back(V[i]);
    return decimated;
}

nonrecursive version:

// nonrecursive version;
std::vector<CPoint> DouglasPeucker_nonrec(const double tol, const std::vector<CPoint>& points) {
    if (points.size() <= 2) return std::vector<CPoint> (); //null_vector;
    double tol2 = tol * tol; //squaring tolerance;
    // 미리 가까이 충분히 가까이 있는 꼭지점은 제거하면 더 빨라짐;
    std::vector<CPoint> vt;
    vt.push_back(points.front()) ;  // start at the beginning;
    for (int i = 1, pv = 0; i < points.size(); i++) {
        int dx = points[i].x - points[pv].x, dy = points[i].y - points[pv].y;
        double dist2 = dx * dx + dy * dy ;
        if (dist2 < tol2) continue;
        vt.push_back(points[i]); 
        pv = i; // 다시 거리를 재는 기준점;
    }
    if (vt.back()!=points.back()) vt.push_back(points.back());  // finish at the end
    points.swap(vt);
    //
    std::vector<bool> mark(points.size(), false); // vertices marking
    std::vector<int> stack(points.size());  // 분할된 라인 처음-끝 저장;
    // 폐곡선이 아닌 경우 처음,끝은 marking; 
    // 폐곡선은 가장 멀리 떨어진 두점 중 하나만 해도 충분
    mark.front() = mark.back() = true;
    int top = -1;
    // 분할 해야할 폴리라인의 양끝점을 스택에 넣음;
    stack[++top] = 0;
    stack[++top] = points.size() - 1;
    while (top >= 0) {
        // 분할을 시도할 구간의 두 끝점을 꺼냄;
        int end = stack[top--];
        int start = stack[top--];
        // 최대로 멀리 떨어진 점;
        double max_distance2 = 0;
        int break_id = -1;
        for (int i = start + 1; i < end; i++) {
            double dsq = pt2SegDist2(points[i], points[start], points[end]);
            if (dsq > max_distance2) {
                max_distance2 = dsq;
                break_id = i;
            }
        }
        // 주어진 임계값 이상 떨어졌으면 꼭지점을 유지하도록 표시;
        if (max_distance2 > tol2) {
            mark[break_id] = true;       
            // 주어진 꼭지점을 기준으로 양쪽을 다시 검사하기 위해 스택에 쌓음;
            stack[++top] = start;
            stack[++top] = break_id;
            stack[++top] = break_id;
            stack[++top] = end;
        }
    }
    // marking 된 꼭지점을 출력;
    std::vector<CPoint> decimated;
    for (int i = 0; i < points.size(); i++)
        if (mark[i]) decimated.push_back(points[i]);
    return decimated;
}