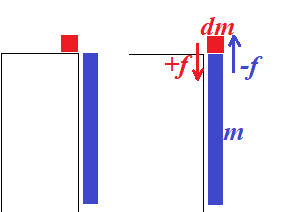
길이가 $L$이고 질량이 $m$인 번지점프줄에 질량이 $M$인 사람이 매달려 낙하한다. 사람이 경험할 수 있는 최대 가속도는?
1. 에너지 보존을 이용: 줄 자체의 무게에 의한 늘어짐은 무시하자. 처음 역학적 에너지는 줄의 위치에너지만 있고, 줄의 무게중심이 낙하지점에서 $L/4$만큼 아래에 있으므로
$$ E_0 = U_0 = -mg \frac{L}{4}$$
낙하를 시작해서 $y$만큼 내려왔을 때 사람의 속력을 $v$라면, 사람 발에 묶인 줄의 속력도 $v$이고, 반대쪽 고정된 줄의 부분은 속력이 $0$이다. 발과 같이 떨어지는 부분의 길이가 $\frac{L-y}{2}$이므로 운동에너지는

$$ K (y)= \frac{1}{2}Mv^2 + \frac{1}{2}\frac{m(L-y)/2}{L} v^2$$
줄의 움직이는 부분의 위치에너지는
$$ U_\text{moving}(y) = - \frac{m(L-y)/2}{L} g \left(y + \frac{L-y}{2}\right) $$
줄의 정지된 부분(아래로 늘어진 길이= $(L+y)/2$)의 위치에너지는
$$ U_\text{still}(y) = -\frac{m(L+y)/2}{L}g \frac{L+y}{4}$$
이다. 역학적 에너지 보존을 이용하면 ($\alpha = m/M$)
$$ v^2 = gy \frac{ 4L + 2\alpha L -\alpha y}{\alpha L -\alpha y + 2L}$$
이 식을 시간에 미분하면 가속도($a=dv/dt$)를 얻을 수 있는데, 앞서 구한 $v$를 넣어서 정리하면
$$ a = g \left( 1 + \frac{\alpha y (4L+2 \alpha L -\alpha y)}{2(\alpha L -\alpha y+ 2L )^2}\right)$$
예상대로 $da/dm>0$이므로 줄의 질량이 커질수록 가속도는 더 커지고, $da/dy>0, ~~y <L$이므로 내려가는 동안 더 가속도가 커져서 사람이 줄의 길이만큼 내려왔을 때 가장 커진다. 물론 그 이상 내려가면 늘어난 줄의 탄성때문에 사람이 내려가는 가속도가 줄어들어서 결국에는 감속의 단계에 이르게 된다.
$$a(y=L) = g \left( 1+ \frac{\alpha (4 +\alpha )}{8}\right)$$
이고, 줄의 무게가 사람 무게와 같을 때($\alpha=1$) 최대 가속도는
$$ a(y=L) = 1.625 g$$
이다.
2. 운동방정식을 이용: 점프를 시작한 후 사람의 발이 묶인 움직일 수 있는 줄의 아래 끝 분은 둥그럽게 굽어지면서 정지를 한다. 이때 속도는 $v$에서 $0$으로 변하는데 평균적으로 완전히 정지할 때까지 평균적으로 $v/2$만큼의 속도를 가진다고 볼 수 있다. 움직이는 부분($m_\text{obj}$)의 질량이 연속적으로 변하므로 운동량 변화를 이용해서 운동방정식을 만들자($dp/dt = F_\text{ext}$).

$$ \left[ (m_\text{obj} + dm_\text{obj}) (v+ dv ) + (-dm_\text{obj})(v/2) \right] - m_\text{obj} v = m_\text{obj} g dt$$여기서
$$m_\text{obj} = M +\frac{m(L-y)/2}{L}, \quad \frac{dm_\text{obj} }{dt} = - \frac{mv}{2L}$$
이를 모두 대입하면
$$a = \frac{dv}{dt} = g + \frac{\frac{1}{2}\alpha v^2}{ \alpha (L-y)+2L}$$
$\frac{dv}{dt} = \frac{1}{2} \frac{dv^2}{dy}$임을 이용하여 적분하면 ($v(0)=0$) 에너지 보존을 이용해서 구한 $v ^2$을 얻고, 이를 다시 $a$식에 대입하면 앞과 동일한 가속도를 얻는다.
그런데 어떻게 중력가속도보다 더 빨리 떨어질 수 있는가?
'Physics > 역학' 카테고리의 다른 글
| 움직일수 있는 반구 위에서 미끄러지는 물체가 떨어지는 각도? (0) | 2024.08.28 |
|---|---|
| 넘어지는 굴뚝이 잘 부러지는 부분은 어디일까? (0) | 2024.08.27 |
| 추의 위치는? (0) | 2024.07.12 |
| 회전할 수 있는 원판이 달린 막대의 진동 주기는? (0) | 2024.05.24 |
| 두 진자의 주기를 비교하면? (0) | 2024.05.24 |