실린더 꼭대기에 정육면체 모양의 물체를 놓은 후 살짝 흔든다. 물체와 실린더 사이의 마찰은 충분해서 미끄러짐은 없다.
A. 물체가 굴러 떨어지지 않고 제자리에서 안정적으로 흔들리기 위한 조건은?
- $a<2R$
- $a<R$
- $a<\frac{1}{2}R$
- $a<\frac{1}{4}R$
B. 흔들림의 폭이 작을 때 주기는?

풀이는 https://kipl.tistory.com/272 하단에서
https://kipl.tistory.com/496 풀이:
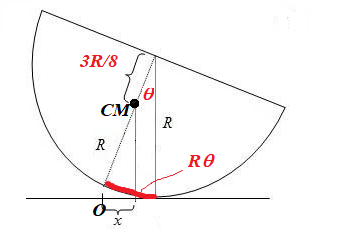
반구의 질량중심은 구 중심에서 $\frac{3}{8}R$ 아래에 있다. 그리고 반구의 중심에 대한 회전관성은 $I_{c} = \frac{2}{5} MR^2$이다(같은 질량의 온전한 구의 회전관성과 같다). 따라서 질량중심을 지나고 지면에 수직인 축에 대한 회전관성은 $I_{cm}=I_c - M(\frac{3}{8} R)^2 = \frac{83}{320} MR^2 $. 수직에 대해 $\theta$ 만큼 굴렸을 때 질량중심의 좌표는 그림에서 보면 (작은 진동만 고려하면 되므로 $\theta^2$ 항까지만 고려하면 된다)
\begin{align}
x &= R \theta - \frac{3}{8}R \sin \theta \approx \frac{5}{8} R \theta \\
y &= R - \frac{3}{8}R \cos \theta \approx \frac{5}{8}R + \frac{3}{16} R \theta^2 .
\end{align}
역학적 에너지가 보존되므로 우선 운동에너지와 위치에너지를 각각 구하면
\begin{align*}
K & =\frac{1}{2} M(\dot{x}^2 + \dot{y}^2 )+ \frac{1}{2} I \dot{\theta}^2 \approx \frac{1}{2} M \Big( \frac{5}{8} R \dot \theta \Big)^2 + \frac{1}{2} \frac{83}{320 } M R^2 \dot{\theta}^2 = \frac{13}{40} MR^2 \dot{\theta}^2 \\
U &=Mgy\approx Mg \frac{5}{8}R + Mg\frac{3}{16}R \theta^2 = \frac{5}{8}mgR + \frac{3}{16} MgR \theta ^2
\end{align*}
또다른 방법으로는 접촉점에 대한 순간회전을 한다는 사실을 이용하면 운동에너지는 쉽게 구할 수 있다. 접촉점에서 반구의 질량중심까지의 거리는
$$d^2 = R^2 + (\frac{3R}{8})^2 -2\frac{3}{8}R^2 \cos \theta=\left( \frac{73}{64}-\frac{3}{4}\cos \theta\right)R^2 $$이므로, 접촉점에 대한 회전관성은
$$ I_\text{IAOR} = Md^2 + \frac{83}{320}MR^2 $$
이고 운동에너지는
$$ K = \frac{1}{2} I_\text{IAOR} \dot{\theta}^2$$으로 주어지는데 위에서 구한 결과와 같다.
역학적 에너지를 시간에 대해 미분해서 운동방정식을 구하면
$$ \ddot{ \theta} + \frac{15}{26} \frac{g}{R} \theta = 0
\quad \Longrightarrow\quad \omega^2=\frac{15}{26}\frac{g}{R} $$
'Physics > 역학' 카테고리의 다른 글
| 흔들리는 반구의 진동 주기(period of an oscillating solid hemisphere) (0) | 2023.01.28 |
|---|---|
| 반구의 회전관성은? (0) | 2023.01.27 |
| 원형 트랙을 돌 때 얼마나 기울여야 하는가? (0) | 2023.01.07 |
| 유체가 채워진 공이 굴러 내려가는 가속도는? (0) | 2023.01.07 |
| 회전하는 두 원판의 공통 물리량은? (2) | 2023.01.06 |



