$$ I = \int_0^\infty \frac{\sqrt{x} \arctan(x)}{x^2 + a^2 }= \frac{\pi}{\sqrt{2a} } \left( \log \frac{\sqrt{a}+1}{\sqrt{a+1}} + \arctan\sqrt{a}\right) ~~a>1$$

$$f(z) = \frac{\sqrt{z} \arctan(z)}{z^2 + a^2 }$$
을 그림과 같은 경로에서 적분을 하자.

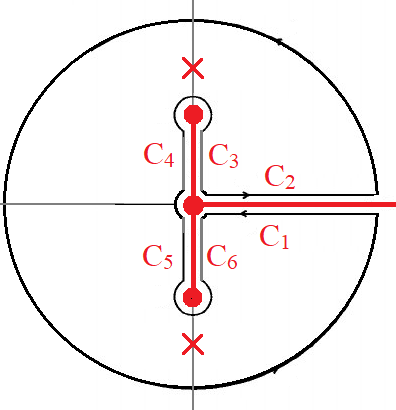
그러면 residue 정리에 의해서
$$ \left( \int_{C_1+C_2} + \int_{C_3 + C_4+C_5 + C_6} \right) f(z)dz = 2\pi i \times\left( \text{Res}f(ia) + \text{Res} f(-ia) \right)$$
여기서 branch point 둘레와 $ C_\infty$에서 적분은 기여가 없다.
$$ \int_{C_1+ C_2 } f(z) = \int_{0}^\infty \frac{\sqrt{x}\arctan(x)dx}{x^2 + a^2} + \int_\infty ^0 \frac{ \sqrt{x}e^{i\pi} \arctan(x) dx }{x^2 + a^2} = 2I $$
$\arctan(z) = \frac{1}{2i} \log \frac{i-z}{i+z}$이므로 $C_3(C_5)$에서$C_4(C_6)$으로 branch cut을 넘어 건널 때 위상이 $2\pi$ 더해지므로 $C_3+ C_4$에서 적분은 $\log$의 위상을 제외한 부분은 상쇄되므로
\begin{gather} \left.\log\frac{i-z}{i+z}\right|_{C_4 || C_6} = \left.\log \frac{i-z}{i+z}\right|_{C_3||C_5}+2\pi i\\ \int_{C_3+C_4} f(z) dz = \int_{C_4}\frac{\sqrt{z} \frac{1}{2i} \times 2\pi i }{z^2 + a^2 }dz =\pi \int_0^1 \frac{ \sqrt{y} e^{i \pi/4} }{ a^2 - y^2 } (idy) \end{gather} \begin{gather}\int_{C_5 + C_6} f(z) dz = \int _{C_5} \frac{\sqrt{z} \frac{1}{2i} \times 2\pi i} {z^2 + a^2} dz = \pi \int_1^0 \frac{\sqrt{y} e^{i3\pi/4} }{a^2 -y^2}(-idy) \end{gather} 따라서
\begin{gather} \int_{C_3+C_4+C_5+C_6} = -\sqrt{2}\pi \int_0^1 \frac{\sqrt{y} dy}{a^2 - y^2}=-\sqrt{2}\pi \int_0^1 \frac{ 2t^2 dt}{a^2 - t^4}\\ = -\sqrt{2}\pi \int_0^1 \frac{dx}{a-x^2} +\sqrt{2}\pi \int_0^1 \frac{dx}{a+x^2} \\=-\frac{\pi}{\sqrt{2a}} \log \frac{\sqrt{a}+1}{\sqrt{a}-1} + \frac{\sqrt{2}\pi}{\sqrt{a}} \arctan \frac{1}{\sqrt{a}} \end{gather}
그리고 $z=ia$에서 $z-i = (a-1) e^{i\pi/2}\to i-z = (a-1) e^{i3\pi/2}$, $z+i= (a+1) e^{i\pi/2}$이므로
$$ \log \frac{i-z}{i+z} = \log\frac{a+1}{a-1} + i\pi$$이고, $z= -ia$에 대해서는 $z-i = (a+1) e^{-i \pi/2}\to i-z= (a+1) e^{i\pi/2}$, $z+i = (a-1) e^{-i\pi/2}$이므로
$$ \log \frac{i-z}{i+z} = \log \frac{a+1}{a-1} +i\pi$$이므로 $z= \pm ia$에서 residue는
\begin{gather} 2\pi i \times \sum \text{Res}= 2\pi i \left(\frac{1}{2i} \frac{ \sqrt{a} e^{i\pi/4} ( \log \frac{a-1}{a+1} + i \pi) }{2ia } + \frac{1}{2i} \frac{\sqrt{a} e^{i3\pi/4} (\log \frac{a+1}{a-1} + i\pi)}{-2ia }\right) \\= \frac{\pi}{\sqrt{2a}} \left( \log \frac{a-1}{a+1} + \pi\right) \end{gather}
따라서 정리하면 ( $ \frac{\pi}{2} = \arctan\frac{1}{\sqrt{a}} + \arctan\sqrt{a}$)
\begin{gather} I =\frac{\pi}{2\sqrt{2a}} \log \frac{(\sqrt{a}+1)^2 }{a+1} +\frac{\pi}{\sqrt{2a}} \left( \frac{\pi}{2} - \arctan\frac{1}{\sqrt{a}}\right) \\ = \frac{\pi}{\sqrt{2a}} \left( \log \frac{\sqrt{a}+1}{\sqrt{a+1}} + \arctan\sqrt{a} \right) \end{gather}
'Mathematics' 카테고리의 다른 글
| Inverse Laplace Transform as Bromwich Integral-6 (0) | 2024.11.10 |
|---|---|
| Integration along a branch cut-033 (0) | 2024.11.09 |
| Integration along a branch cut-031 (0) | 2024.11.06 |
| Integration along a branch cut-030 (0) | 2024.11.02 |
| Inverse Laplace Transform as Bromwich Integral-5 (0) | 2024.10.29 |



