$$ \frac{1}{2\pi i} \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{e^{st} ds}{\sqrt{s^2 -1}} = I_0(t)\\ \frac{1}{2\pi i} \int_{\gamma-i\infty}^{\gamma + i \infty} \frac{e^{st}ds }{\sqrt{s^2 +1}} = J_0 (t)$$

$$g(z)= \frac{e^{zt}}{\sqrt{z^2-1}}$$을 적분하기 위해서 그림과 같이 Browmwich contour를 선택하자. 위상은 $$ -\pi \le \arg(z-1), ~\arg(z+1) \le \pi $$
$\oint g(z) dz = 0$이므로
$$ I= \frac{1}{2\pi i} \int_{\gamma - i\infty}^{\gamma + i \infty} \frac{e^{st}ds}{\sqrt{s^2 - 1}} = - \sum_k \frac{1} {2\pi i} \int_{C_k} \frac{e^{zt}dz}{\sqrt{z^2-1}}$$
$C_2$에서 $z-1 = (1-x) e^{i \pi}$, $z+1 = (1+x) e^{i0}$이므로
$$ \int_{C_2} = \int_{-1}^1 \frac{e^{xt} dx}{ \sqrt{1-x^2} e^{i \pi/2} }= -i \int_{-1}^1 \frac{ e^{xt}dx}{\sqrt{1-x^2}} $$
$C_4$에서 $z-1= (1-x) e^{-i \pi}$, $z+1=(1+x) e^{i 0}$이므로
$$ \int_{C_4} = \int _{1}^{-1} \frac{e^{xt}dx}{ \sqrt{1-x^2}e^{-i\pi/2}} = -i \int_{-1}^1 \frac{ e^{xt}dx}{\sqrt{1-x^2}} $$
이고 $\int_{C_1} = \int_{C_3}= 0$이므로
$$ I = \frac{1}{\pi} \int_{-1}^{1} \frac{e^{xt} dx} {\sqrt{1-x^2}}$$
$ x= \cos \theta$로 치환하면
$$I= \int_{0}^\pi e^{t \cos \theta} d \theta = \frac{1}{\pi}\sum_{k=0}^\infty \int_{0}^{\pi } \frac{ (t \cos \theta)^k d \theta }{ k!} \\ = \frac{1}{\pi} \left[ \pi + \pi \frac{1}{2} \frac{t^2}{2!}+ \pi \frac{3}{4} \frac{1}{2} \frac{t^4}{4!} + \pi\frac{5}{6}\frac{3}{4}\frac{1}{2} \frac{t^6}{6!}+\cdots \right] \\ = 1+ \frac{t^2}{2^2}+ \frac{t^4}{2^2 4^2 }+ \frac{t^6}{2^2 4^2 6^2}+\cdots = \sum_{k=0}^ \infty \frac{(\frac{t}{2})^{2k}}{(k!)^2} \\= I_0(t)$$
$I_0(t)$는 modified Bessel function of the first kind and zero order.

Note: $$ {\cal L }^{-1} \left[\frac{1}{\sqrt{s^2 + 1}}\right] = J_0(t)$$

$$ -\frac{\pi}{2} \le \arg(z+i), ~\arg(z-i) \le \frac{3\pi}{2}$$
residue 정리에 의해서
$$ I = \frac{1}{2\pi i}\int_{\gamma - i \infty} ^{\gamma + i \infty }\frac{ e^{st}ds}{\sqrt{s^2 + 1}} = -\sum_k \frac{1}{2\pi i} \int_{C_k} \frac{e^{zt} dz}{ \sqrt{z^2+1}}$$
$C_2$에서 $z- i = (1-y) e^{-i\pi/2}$, $z+i = (1+y) e^{\pi/2}$이므로
$$ \int_{C_2} = \int_{1}^{-1} \frac{ e^{i yt} (idy)}{ \sqrt{1- y^2}} = -i \int_{-1}^1\frac{ e^{-iyt}d y}{\sqrt{1-y^2}}$$
$C_4$에서 $z-i=(1-y) e^{i 3\pi/2}$, $z+i= (1+y) e^{i\pi/2}$이므로
$$ \int_{C_4} = \int_{-1}^{1} \frac{e^{i yt}(i dy)}{\sqrt{1-y^2} e^{i\pi}} =- i\int_{-1}^{1} \frac{e^{iyt} dy }{\sqrt{1-y^2}} $$
따라서 $$\int_{C_2 +C_4} = -2i \int_{-1}^2 \frac{\cos(yt)dy}{\sqrt{1-y^2}}$$
$$ I = \frac{1}{\pi} \int_{-1}^{1} \frac{ \cos(yt) dy}{\sqrt{1 -y^2}}= \frac{1}{\pi} \int_{-\pi}^{\pi} \cos( t \sin \theta) d \theta = J_0(t)$$
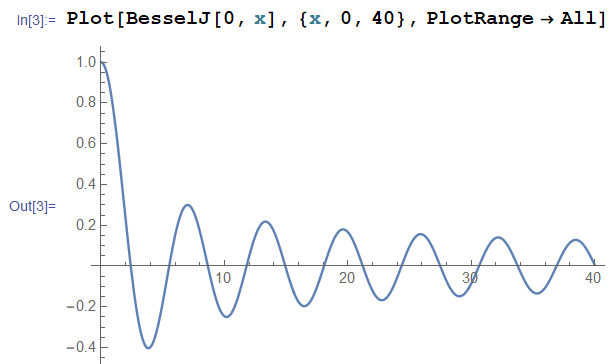
$J_0(t)$는 Bessel function of the first kind and zero order.
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-031 (0) | 2024.11.06 |
|---|---|
| Integration along a branch cut-030 (0) | 2024.11.02 |
| Integration along a branch cut-029 (0) | 2024.10.28 |
| Fourier transform inversion using a contour integral (0) | 2024.10.26 |
| Inverse Laplace Transform을 이용한 무한 LC Ladder Circuit에서 Step Respose (0) | 2024.10.24 |



