Geometry & Recognition

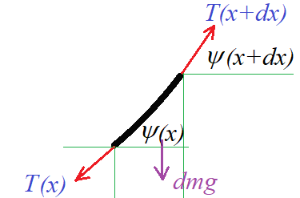
단순진자는 원호 위에서 반복운동을 한다. 수직에 대해 벌어진 각이 $\theta$일 때 각에 대한 운동 방정식은

$$ \ddot \theta = - \frac{g}{L} \sin \theta.$$

진폭이 작은 경우 ($|\theta| \ll 1$) 윗 식은 용수철 진자의 운동인 단순 조화 운동이 되고 주기는 진폭에 무관하게 일정한 값을 가지게 된다:

$$ \ddot \theta \approx - \frac{g}{L} \theta    \quad \Leftrightarrow  \quad \ddot{x} = - \omega^2 x.$$

그러나 단순진자의 진폭이 일정 이상 커져 작은 각 근사에서 벗어나면 주기는 진폭에 따라 달라짐이 잘 알려져 있다.

진자가 원호가 아닌 다른 곡선 위를 움직일 때 주기가 진폭에 무관하게 주어질 수 있는지 알아보자. 이 경우는 각보다는 용수철 진자처럼 평형점에서 움직인 거리를 이용해서 운동을 기술하는 것이 더 편리하다. 단순진자의 경우 평형점에서 잰 원호의 거리를 $s$라면 $s=L \theta$로 표현되고 작은 각 근사에서 운동 방정식은 
$$ \ddot {s} =-\omega^2  s.$$

이제 진자가 움직이는 곡선에 어떤 제약이 들어오는지 살펴보자. 먼저 움직인 거리에 대한 운동 방정식은 단순조화운동식과 같아야 하므로 위의 형태는 변하지 않아야 한다. 진자가 움직이는 곡선이 $y(x)$로 표현되면 평형점($x=0$) 에서 움직인 거리($x <0$이면 움직인 거리의 음수)는

$$s = \int_0^x \sqrt{ 1+ \Big(\frac{dy}{dx}\Big)^2} dx$$

로 표현된다. $s$에 대한 단순 조화 진동은 위치 에너지가 $U(s) = \frac{1}{2} m\omega^2 s^2$인 경우에 해당하는데 진자는 중력의 영향을 받으므로 이 위치 에너지는 결국 중력 위치 에너지 표현되어야 한다: 

$$ \frac{1}{2} m\omega^2 s^2 = mgy.$$

양변을 $x$에 대해 미분한 후 정리하면

$$ \frac{dy}{dx} = \sqrt{ \frac{2\omega^2 y}{  g - 2\omega^2 y}}.$$

이 방정식을 풀기 위해서 새로운 매개변수 $\psi$를 도입하는데, $dy/dx$가 접선의 기울기이므로 $dy/dx=\tan (\psi/2)$로 놓으면(각은 나중을 위해서 2배 한 것임), 

$$   \sin^2(\psi/2) = \frac{2\omega^2 }{g} y  \quad \Longrightarrow \quad y = \frac{g}{4\omega^2} (1 - \cos\psi).$$

$dx/d\psi  = (dy/d\psi) / (dy/dx)$을 계산해서 적분하면 ($x(\psi=0)=c$)

$$  \frac{dx}{d\psi} = \frac{g}{4\omega^2} (1+\cos \psi)\quad \Longrightarrow \quad x= \frac{g}{4\omega^2} (c+\psi + \sin \psi).$$

이제 $\psi \rightarrow \pi +\psi, c=-\pi $로 변수 치환을 하면(이 경우 $dy/dx= -\cot(\psi/2)$) 진자가 움직여야 하는 곡선이 우리가 잘 알고 있는 cycloid임을 알 수 있다.

$$\begin{matrix} x= a ( \psi -\sin \psi )  \\ y=a(1 + \cos \psi)\end{matrix} ~~~~\left(a \equiv \frac{g}{ 4\omega^2}\right).$$

이 곡선은 반지름 $a$인 원이 $y=2a$인 수평선을 따라 구를 때, 원이 처음 $y=2a$와 접하는 점이 그리는 자취를 나타내고, $\psi$는 원의 중심과 그 점이 잇는 선분이 수직과 이루는 각이다.

Cycloid 모양을 결정하는 $a$가 정해지면 진자의 각진동수 $\omega=\sqrt{g/4a}$를 알 수 있고 주기는 $$T=\frac{2\pi}{\omega }= 4\pi \sqrt{\frac{a}{g}}$$

로 주어진다. 곡선이 주어졌으므로 처음 $y=h$에서 출발할 때 구체적으로 주기를 확인해 보자. 역학적 에너지가 보존되므로 

\begin{align} E &=\frac{1}{2} m \Big( \frac{ds}{dt}\Big)^2 +\frac{1}{2} m \omega^2 s^2 \\&= \frac{1}{2} \Big( \frac{ds}{dt}\Big)^2 + mgy = mgh\\ \Longrightarrow~~ dt &= \pm \frac{ds}{\sqrt{2g(h-y)}} \end{align} 주기는 $y=h$에서 출발해서 바닥에 도달하는데 걸리는 시간의 4배이므로 \begin{align} T &= 4 \int_0^h \frac{ds}{\sqrt{2g(h-y)}} \\ &= \frac{4}{\sqrt{2g}} \int_{\pi/2}^{\psi_0} \frac{-4a d \cos (\psi/2)}{\sqrt{2a[\cos^2(\psi_0/2) - \cos^2(\psi/2)]}} \\ &=4\pi \sqrt{\frac{a}{g}}\end{align} 즉, 주기는 출발 높이에 무관하게 주기가 일정함을 알 수 있다.

공을 cycloid 모양으로 생긴 골짜기에 굴리면 등시운동을 하지만, 그럼 등시진자는 어떻게 만들수 있을까? 이 문제도 역시 cycloid로 해결이 된다. 위에서 구한 cycloid를 y방향으로 $-2a$ 만큼 평행이동시킨 모양을 고려하자. $$ \begin{matrix} x = a (\psi - \sin \psi) \\ y = a( \cos \psi - 1)\end{matrix}$$이 식으로 표현된 cycloid 모양의 천정을 만든 후(그림의 실선), 원점(꼭대기)에 길이 $L$인 줄을 고정시키고 끝에는 무거운 추를 매단다. 추을 진동을 시키면 줄의 일부는 cycloid 모양의 천정을 따라 접하고 나머지 부분은 직선의 형태로 된다.

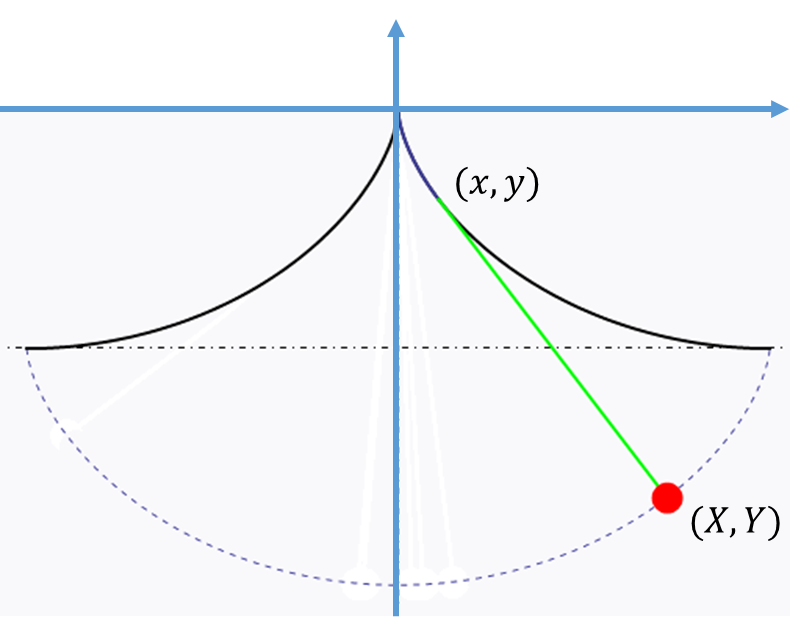
줄과 cycloid가 접하는 끝지점을 $(x, y)$라 할 때 접하는 부분의 줄의 길이는 $$ \ell = \int_0^\psi ds = a \int_0^\psi \sqrt{ (1-\cos \psi')^2 + (\sin \psi')^2} d\psi' = 4a [1- \cos (\psi/2)]$$로 주어진다. $(x, y)$ 이후의 줄은 접선의 방향으로 나간다. 접선의 기울기를 $\frac{dy}{dx}=\tan \phi$로 놓으면 $\phi=\psi/2 - \pi/2$이고, 직선 부분의 길이가 $L- \ell$이므로 추의 위치는 $$ \begin{matrix} X = x + (L- \ell)\cos \phi = (L - 4a) \cos \phi + a(\psi + \sin \psi) \\ Y = y+(L-\ell) \sin \phi =(L-4a)\sin \phi - a(3+ \cos \psi)  \end{matrix}$$로 주어진다. 줄의 길이를 $L=4a$로 선택하면 추의 위치 $(X, Y)$도 (평행이동된) cycloid(그림의 점선) 상에서 움직임을 알 수 있다. 따라서 이렇게 만들어진 추의 주기는 등시성을 갖는다. $$ \text{추의 위치:}~~\left\{ \begin{array}{l} X= a (\psi + \sin \psi)  \\ Y = -a( 3 + \cos \psi)\end{array}\right. $$

다시 이 진자의 주기를 구체적으로 확인하면, 

$$ds=  \sqrt{dX^2 + dY^2} = \pm a\sqrt{2(1+\cos \psi)} {d\psi} $$

이고, 역학적 에너지가 보존되므로($\Delta y = a (\cos\psi - \cos \psi_0)$)  

\begin{align} \tau &= 4 \int_{0}^{\psi_0} \frac{ds}{\sqrt{2g \Delta y} }  \\  &= 4\sqrt{\frac{a}{g}} \int_{0}^{\psi_0} \sqrt{\frac{1+\cos \psi}{\cos \psi - \cos\psi_0}} d\psi  \\ &= 4\pi \sqrt{ \frac{a}{g}} = 2\pi \sqrt{ \frac{L}{g}}\end{align}이다. 즉, 줄의 길이가 $L=4a$인 단진자가 작은 진동을 할 때의 주기와 동일하고, cycloid에서 미끄러지면서 운동하는 물체의 진자와도 같음을 알 수 있다.

체인이나 줄을 느슨한 상태로 양끝을 고정시킬 때 모양은 포물선처럼 보이지만 실제로는 그렇지 않고 현수선(catenary)라고 불리는 곡선이다. 양끝을 고정시킨 줄을 보자.

늘어진 줄에는 자신의 무게를 지탱하기 위해서 장력이 걸린다. 그런데 중력이 수직방향으로 걸리므로 장력은 줄의 위치에 따라 달라져야 한다.  수평방향은 움직임이 없으므로 장력의 수평 성분은 모두 같아야 하는데, 줄의 가장 아래로 처진 부분의 접선방향이 수평이므로 이 지점에서 장력($T_0$)와 같아야 한다. 줄의 선밀도가 $\lambda$이고, 가장 아래 지점을 기준으로 곡선의 길이를 $s$라고 하자. 현수선의 수평 위치를 $x$, 수직 위치를 $y$로 하면 $y$는 $x$의 함수로 생각할 수 있고, 가장 아랫부분($x=0$으로 잡자)에서 잰 줄의 길이는

$$s =\int\sqrt{dx^2 + dy^2} =  \int_{0}^x \sqrt{1 + (dy/dx)^2} dx$$

로 쓸 수 있다.

그러면 $(x, y)$에서 줄의 장력을 $T$, 접선이 이루는 각도를 $\psi$라면, 힘의 평형 조건에서

\begin{gather} T \cos \psi = T_0 \\ T \sin \psi = \lambda s g . \end{gather}

따라서 접선의 기울기는

$$ \frac{dy}{dx} = \tan \psi = \frac{\lambda gs }{T_0} = \frac{s}{a}= \frac{1}{a} \int_0^{x} { \sqrt{ 1+\Big( \frac{dy}{dx}\Big)^2}} dx, \quad a \equiv \frac{T_0}{\lambda g}$$

이 식은 $y(x)$에 대한 미분-적분 방정식 형태이므로 미분 방정식으로 바꾸기 위해서 한번 더 미분을 하면 

$$ \frac{d^2 y}{dx^2}  = \frac{1}{a} \sqrt{1 + \Big(\frac{dy}{dx}\Big)^2 }.$$

한번 적분하면 ($\frac{dy}{dx} (x=0)=0$)

$$ \frac{dy}{dx}  =\sinh (x/a).$$ 

다시 적분하면 

$$ y = a \cosh( x/a) + C$$

을 얻는 데, 원점을 이동해서 현수선의 가장 아랫부분이 ($0,a$)가 되도록 조정하면 $C=0$이 된다. 현수선은 선밀도와 꼭지점에서의 장력 비 $a$로 모양이 결정된다. 이 값은 한 지점에서 꼭짓점까지 수평거리($x$)와 기울기를 측정하면 결정할 수 있다: 특징 1번. 그리고 $|x| \ll a$일 때

$$y=  a\left[ 1 + \frac{1}{2}\Big(\frac{x}{a}\Big)^2 + \frac{1}{24}\Big( \frac{x}{a}\Big)^4+...\right] $$

이므로 꼭짓점 근방에서는 포물선으로 근사가 가능하다.

몇 가지 특징:

1. 접선의 기울기:  $\tan \psi =\frac{dy}{dx}= \sinh(x/a)$. 

2. 곡선의 길이: $s = a \tan\psi = a \sinh( x/a)$.

3. $y^2 = a^2+ s^2 ~~\rightarrow ~~ y = a\cosh(x/a) = a\sec(\psi)$.

4. 장력: $T = \lambda g \sqrt{a^2 + s^2} =\lambda g \cosh (x/a)= \lambda g y$. 

5. 현수선의 길이($s$)를 매개변수로 선택하면,

$$\frac{dx}{ds} = \frac{1}{ds/dx}= \frac{1}{\sqrt{1 + (dy/dx)^2} }= \frac{a}{\sqrt{a^2 + s^2}},$$

$$ \frac{dy}{ds} = \frac{dy/dx}{ds/dx}=\frac{s}{\sqrt{a^2+s^2}},$$

따라서 $(dx/ds)^2 + (dy/ds)^2 = 1$임을 알 수 있다.

6. $\frac{dx}{d s} = \frac{1}{a}   \cos^2(\psi)\frac{dx}{d\psi} = \cos(\psi) ~~\rightarrow~~ \frac{dx}{d\psi} = a \sec{\psi} $  이므로 $x= a \ln ( \sec(\psi) + \tan(\psi))$

Note: 미분방정식의 유도를 local version으로 바꾸자. 줄의 장력의 $x$의 함수로 볼 수 있고, 그림에서 힘의 평형을 적용하면, 우선 수평방향에 대해서

$$ \sum F_x = T(x+dx) \cos[ \psi(x+dx)] - T(x) \cos [\psi(x)]=0$$ 

이 식은 장력의 수평성분은 어디서나 같음을 의미하므로 이 값을 꼭지점($\psi=0$)의 값 $T_0$로 고정하자.

수직방향에 대해서는

$$ \sum F_y = T(x+dx) \sin[ \psi(x+dx)] - T(x) \sin[\psi(x)] -dm g=0$$

$T(x+dx)$와 $T(x)$을 소거하고 정리하면

$$  \tan  [\psi(x+dx)] -\tan[\psi(x)] = \frac{dm g}{T_0} = \frac{\lambda g}{T_0} \sqrt{dx^2+dy^2}.$$ 

그런데 $dy/dx = \tan(\psi)$이므로 

 $$ \tan[\psi(x+dx)]- \tan[\psi(x)] = dx \frac{d}{dx} \tan(\psi) =    \frac{d^2y}{dx^2 }dx$$

정리되어 현수선 방정식을 얻을 수 있다.