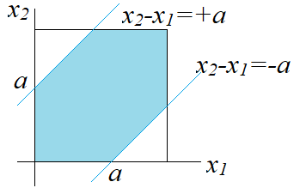줄에 걸리는 장력을 줄의 단면적으로 나눈 값이 stress ($\sigma = T/A$)는 균일한 줄에서는 일반적으로 일정할 수 없다. 현수선에서 줄에 걸리는 stress를 유지하려면 줄의 단면적을 가변적으로 만들면 가능하다. 이 경우 현수선 중심선의 모양 $y(x)$가 어떻게 주어지는 알아보자. 현수선의 밀도가 $\rho$, 꼭짓점으로부터 떨어진 거리가 $s$인 지점의 단면적이 $A(s)$일 때, 힘의 평형 조건에서
$$ \sum F_x = T\cos \psi - T_0 = 0 ,$$
$$ \sum F_y = T\sin \psi - \int \rho g A(s) ds = 0. $$

여기서 $T_0$는 장력의 수평성분으로 꼭짓점에서 장력을 의미한다. 위 식에서 $T$를 소거하여 정리하면
$$ y' = \tan\psi = \rho g \int \frac{A(s) ds}{T_0}$$
을 얻는다. stress가 일정하다는 조건 $ \sigma = T/A(s)$에서 $A(s) =T(s)/\sigma = T_0/\sigma \cos \psi$로 치환하면
$$ y' = \frac{\rho g }{\sigma} \int \frac{ds}{\cos \psi}.$$
양변을 $s$로 미분하면
$$ \text{LHS}= \frac{d}{ds} y' = \frac{dx}{ds} y'' = \frac{1}{ds/dx} y'',$$
$$\text{RHS} = \frac{\rho g}{\sigma} \frac{1}{\cos\psi}.$$
$\tan \psi = dy/dx$ 이므로 $\cos\psi = 1/\sqrt{1+ (dy/dx)^2}$, 그리고 $ds/dx = \sqrt{1+ (dy/dx)^2}$ 이므로
곡선이 만족해야 하는 방정식은
$$ y'' = \frac{\rho g}{\sigma} (1 + (y')^2 )$$
으로 주어진다.
꼭짓점이 $x=0$을 통과하게 선택하면 $y'(x=0)= 0$이므로 위식을 적분하면
$$ y' = \tan \Big( \frac{\rho g}{\sigma} x \Big).$$
꼭짓점이 원점에 있게 좌표를 잡으면, $y(x=0)=0$, 위 식을 적분해서
$$ y = -\frac{\sigma}{\rho g} \log \cos \Big( \frac{\rho g}{\sigma} x\Big) $$
을 얻는다. 꼭짓점 근방에서 위 곡선은 포물선으로 근사된다.
$$ y \approx \frac{\rho g}{ 2\sigma} x^2 + ....$$
Catenary
체인이나 줄을 느슨한 상태로 양끝을 고정시킬 때 모양은 포물선처럼 보이지만 실제로는 그렇지 않고 현수선(catenary)라고 불리는 곡선이다. 양끝을 고정시킨 줄을 보자. 늘어진 줄에는 자신의
kipl.tistory.com
'Mathematics' 카테고리의 다른 글
| Catenary: Rolling Parabolas (0) | 2022.02.03 |
|---|---|
| Catenary: rolling square wheels (0) | 2022.02.02 |
| Catenary: Variational Approach (0) | 2022.01.29 |
| Generate uniformly random points within a circle (0) | 2022.01.29 |
| Mean distance between two randomly chosen points in unit square (0) | 2022.01.28 |