도넛의 표면은 수학적으로 torus와 같은 구조를 가진다. 반지름 $r$이고 길이가 $2\pi R$인 원통을 둥글게 구부리면 그림의 오른쪽과 같은 토러스를 만들 수 있다.
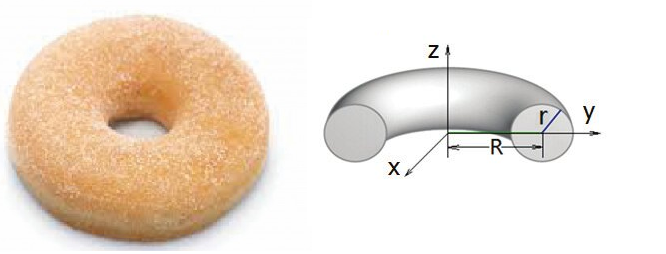
수학적으로는 중심이 $z$축에서 $R$만큼 떨어진 반지름 $r$인 원을 $z$에 대해 회전을 시켜서 만들 수 있다. 이 사실을 이용하면 토러스의 표면적은 쉽게 구할 수 있다. $z$축에 대한 회전각을 $\theta$, $x(y)-z$평면에 회전각을 $\varphi$라고 하자. 그리고 $\theta$방향으로 일정한 간격 $d \theta$만큼으로 토러스를 자르면 잘려진 부분의 표면은 축에 가까운 쪽은 폭이 $(R-r)d\theta$, 먼쪽은 폭인 $(R+r)d \theta$인 고리띠의 모양을 한다. 사이에서 고리띠의 폭은 $(R+r\cos \varphi)d \theta $임을 쉽게 알 수 있다.

따라서 이 고리띠의 미소면적 $(R+r\cos \alpha) d\theta \times (rd\varphi)$을 $\varphi$에 대해 적분하면 $$ \text{고리띠 면적}= dA = \int_0^{2\pi}(R + r\cos\varphi) rd\varphi = 2\pi r R d\theta$$이 결과를 $\theta$에 대해 적분하면 토러스의 면적을 얻을 수 있다.
$$ \text{Area of torus} = \int_0^{2\pi} 2\pi rR d \theta = 4\pi ^2 rR$$
좀 더 수학적으로 하면 2차원 표면의 법선벡터를 $\vec v$라면 면적은
$$ \text{Area} = \iint |\vec{v}| dA$$
인데, 앞에서 도입한 $\theta, \varphi$을 이용하면
\begin{gather} \vec{r} = ( (R+r \cos \varphi)\cos \theta, (R+ r\cos \varphi)\sin \theta, r\sin\varphi) \\ \to | \vec {v}| = \left|\frac{\partial \vec{r}}{\partial \theta} \times \frac{\partial \vec{r}}{\partial \varphi}\right| = r (R+ r\cos \varphi) \\ \text{Area} = \int_0^{2\pi} \int_0^{2\pi} r (R+r\cos \varphi) d\theta d\varphi = 4\pi^2 rR \end{gather}
토러스의 부피는 앞에서 고리띠(기울어지게 잘린 미소 실린더: 중심에서 높이=$Rd\theta$)의 부피가 $dV=\pi r^2\times Rd\theta$이므로
$$ \text{Volume} = \int _0^{2\pi} \pi r^2 R d\theta = 2\pi^2 r^2 R$$
'Mathematics' 카테고리의 다른 글
| Integrate [log(1+x)/x, {x, -1, 1}] (0) | 2024.11.13 |
|---|---|
| Integration along a branch cut-034 (0) | 2024.11.10 |
| Inverse Laplace Transform as Bromwich Integral-6 (0) | 2024.11.10 |
| Integration along a branch cut-033 (0) | 2024.11.09 |
| Integration along a branch cut-032 (0) | 2024.11.07 |




