가벼운 막대로 연결된 두 물체 B, C에 그림과 같이 물체 A가 $v_0$로 다가와 정면으로 탄성충돌을 한다. 충돌 후 각 물체의 속력은? 단, 세 물체의 질량은 모두 같다.
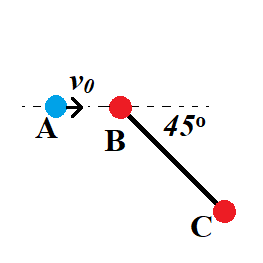
힌트: 정면충돌을 하므로 충돌 후 A의 속도성분 $v_1~(EE)$는 충돌 전과 나란한 방향이고, B의 속도는 막대방향 성분 $v_2~(SE)$와 막대에 수직인 성분 $v_3~(NE)$로 분해하자. 충돌 직후에서 막대의 장력에 의해서 C는 $v_2$의 막대방향 속도성분을 가진다. A와 B의 충돌이 탄성적이므로 충돌 전후의 상대속도의 크기가 같아야 한다.
$$ v_0 - 0 = \frac{v_2 + v_3}{ \sqrt {2}} - v_1 $$
외력이 없으므로 y축 방향 운동량이 보존되고,
$$ 0 = -\frac{mv_2}{\sqrt{2}} + m\left( - \frac {v_2}{\sqrt {2}} + \frac {v_3}{\sqrt {2}}\right)~~~\to~~~ v_3 = 2v_2$$
또한 x축 방향의 운동량도 보존되므로
$$mv_0 = mv_1 + m \left( \frac{v_2}{\sqrt{2}} + \frac {v_3}{ \sqrt {2}}\right)+ m \frac {v_2}{\sqrt {2}}~~~\to~~~ v_0 = v_1 + \frac {4}{\sqrt {2}} v_2 $$
따라서 미지수 $v_1, ~v_2, ~v_3$에 식 3개가 주어졌으므로 풀면
$$ v_1 = - \frac{v_0}{7},~~~v_2 = \frac {2\sqrt {2}}{7} v_0,~~~v_3 = \frac {4\sqrt {2}}{7} v_0$$
'Physics > 역학' 카테고리의 다른 글
| 충돌 직후 줄에 걸리는 장력은? (0) | 2025.03.11 |
|---|---|
| 추가 원통을 감기 시작할 때 각가속도는? (0) | 2025.03.10 |
| 충돌 후 충분한 시간이 지났을 때 운동에너지는? (0) | 2025.03.09 |
| 실린더가 정상상태가 되는 과정에서 잃어버린 운동에너지는? (0) | 2025.03.09 |
| 회전하는 물체에 연결된 추의 가속도는? (0) | 2025.03.08 |




