마찰이 없는 테이블 중앙에 있는 구멍을 통해 두 물체 A와 B가 줄로 연결되어 있다. B를 고정한 채 A를 일정한 각속도 $\omega_0$로 회전시킨다. 이때 구멍에서 A까지 거리는 $r_0$이다. 이제 B가 움직일 수 있게 놓아둔다면 그 순간 B의 가속도는?
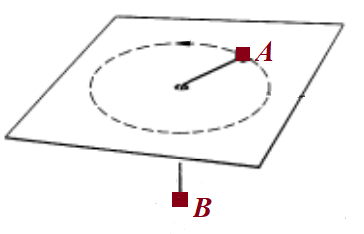
힌트: 줄에 걸리는 장력을 $T$라면 B의 운동방정식은
$$ m_B g - T = m_B \ddot {z} ~~~(+z: \downarrow)$$
A의 운동은 radial 방향과 접선방향으로 운동으로 구분할 수 있는데 A에 작용하는 힘은 장력뿐이므로
$$ -T = m_A( \ddot{r} - r \omega^2 )~~~\text {and}~~~ r \alpha + 2 \dot {r} \omega = 0$$
A와 B는 줄로 연결되어 있으므로 $z+ r = const~\to ~ \ddot{z}=- \ddot {r}$이므로
$$\ddot {z} = \frac {m_B g - m_A r \omega^2}{m_A + m_B}$$
인데, $r\to r_0$, $\omega\to \omega_0$을 대입하면
$$ \ddot{z}(0) = \frac {m_B g - m_A r_0 \omega_0^2}{m_A + m_B}$$
A에 작용하는 외부토크가 없으므로 각운동량이 보존된다: $\omega r^2 = const$. $r$에 대한 방정식으로 바꿔 쓰면
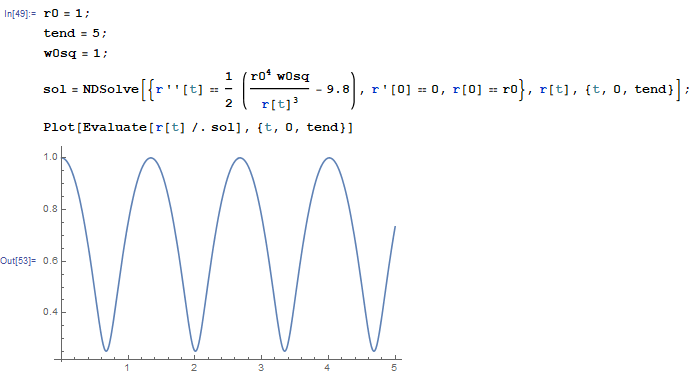
$$ \ddot{r} = \frac{m_A \omega_0^2 r_0^4/ r^3 -m_B g}{m_A +m_B}$$이 미분방정식을 수치적으로 풀 수 있다. $m_B$에 걸리는 중력은 구멍에서 $m_A$까지 길이를 짧게 하려고 하지만, 각운동량 보존때문에 줄이 짧아지면 centrifugal barrier가 높아지게 되므로 다시 길이가 늘어나는 운동을 반복한다. 이는 행성의 타원궤도 운동과 유사한 특성을 가진다.
'Physics > 역학' 카테고리의 다른 글
| 충돌 후 충분한 시간이 지났을 때 운동에너지는? (0) | 2025.03.09 |
|---|---|
| 실린더가 정상상태가 되는 과정에서 잃어버린 운동에너지는? (0) | 2025.03.09 |
| 막대와 같이 회전하는 고리가 끝에 도달했을 때 (0) | 2025.03.08 |
| 별의 절반이 나머지 절반을 당기는 힘 (0) | 2025.03.07 |
| 반구에서 미끄러지기 시작한 줄의 장력이 최대인 지점은? (0) | 2025.03.04 |




