그림과 같이 매끄러운 바닥에 놓인 길이 $L$인 막대의 왼쪽 끝이 길이 $D$로 느슨하지 않은 줄에 연결되어 있다. 막대의 오른쪽 끝에 같은 질량의 총알이 $v_0$로 다가와 박힌다. 막대는 반시계방향으로 회전을 하려고 하기 때문에 줄이 팽팽해진다. 이때 줄에 걸리는 장력은?
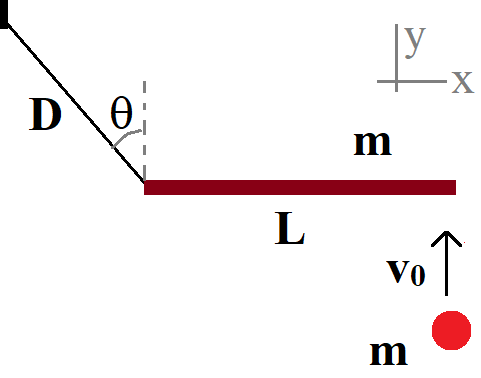
힌트: 줄이 팽팽해지면서 장력을 작용하므로 줄방향의 운동량은 보존이 안되고, 줄에 수직인 방향의 운동량은 보존된다. 따라서 충돌직후 총알 박힌 막대의 질량중심이 움직이는 속도를 $v_\bot$ 과 $v_\parallel$로 나누면
$$\text {줄에 수직방향 운동량 보존:}~~~ 2m v_\bot = mv_0 \sin \theta$$$$\to~~~ v_\bot = \frac {1}{2} m v_0 \sin \theta $$
충돌직후 총알 박힌 막대의 질량중심(왼쪽 끝에서 $\frac {3}{4} L$)을 기준으로 회전운동을 시작하는데 이때 각속도를 $\omega$라고 하자. 그리고 막대왼쪽 끝 줄에 연결된 부분(A)은 줄 때문에 충돌직후 순간적으로 회전을 한다. A지점의 속도($v_A$)는 질량중심의 속도와 질량중심에 대한 회전각속도로 표현할 수 있는데, 줄이 안 늘어나므로 줄방향 성분이 없어야 한다:
$$\text {A의 줄방향 속도 성분 = 0:}~~~ 0 = v_\parallel - \frac {3L}{4} \omega \cos \theta$$$$ \to~~~ v_\parallel = \frac {3L}{4} \omega \cos \theta$$
줄에 수직인 성분을 질량중심 속도와 회전각속도를 이용해서 표현하면,
$$\text{A의 줄에 수직 속도 성분:}~~~~~~~$$$$v_A = -v_\bot +\frac {3L}{4} \omega \sin \theta= -\frac {1}{2} v_0\sin \theta + \frac {3L}{4} \omega \sin \theta ~~~~(*)$$
그다음으로 $A$ 점에 대한 토크가 없으므로 각운동량이 보존된다. 초기 각운동량은
$$ L_i = mv_0 L$$
충돌직후 각운동량은 총알 박힌 막대의 질량중심에 대해서 $\omega$로 회전하고, 질량중심이 또 움직이므로 이 둘을 고려해야 한다. 질량중심에 대한 회전관성은 $$I_{cm} = \frac {1}{12} mL^2 + m \frac {L^2}{16} + m\frac {L^2}{16}= \frac {5}{24} mL^2$$ 로 주어지므로 충돌직후 각운동량은
$$L_f = I_{cm} \omega + (2m) \frac {3L}{4} (v_\bot + v_\parallel)_y$$
$$ = \frac{5}{24} mL^2 \omega + (2m) \frac {3L}{4} ( v_\bot \sin \theta + v_\parallel \cos \theta) $$
$$= \frac {5}{24} mL^2 \omega +\frac {3mL^2}{2} \left( \frac {3L}{4}\omega - v_A \sin \theta \right)$$이다. 각운동량 보존($L_i = L_f$)에서
$$ v_0 = \frac{3}{2} \left( \frac {3L}{4}\omega - v_A \sin \theta \right) + \frac {5}{24} L\omega~~~~(**)$$
이므로 (*) 식과 연립해서 $v_A$와 $\omega$을 구할 수 있다.
$$ v_A =\frac {2v_0 \sin \theta}{32-27 \sin^2 \theta},~~~\omega L = \frac {6v_0 ( 4 - 3\sin^2 \theta)}{32 - 27 \sin^2 \theta}$$
팽팽해진 줄 때문에 A점은 순간적으로 회전운동을 하므로 줄과 나란한 방향의 가속도 성분은 구심가속도로 표현된다.
$$ ({a}_A)_\parallel = \frac {v_A^2}{D}$$
그런데 A점에 작용하는 힘은 장력뿐만 아니라 막대의 다른 부분이 작용하는 힘도 있으므로 구심력이 장력이 되지 못한다. 막대에 작용하는 외력이 장력뿐이므로 막대의 질량중심 가속도는
$$ \text{cm 가속도:}~~{a} = \frac {{T}}{2m} ~~~~\text {parallel to the string}$$ 또 장력은 질량중심에 대한 토크(시계방향 회전)를 형성하므로
$$ \tau = -\frac {3L}{4} T \cos \theta = \frac {5}{24} mL^2 \alpha ~~~\to ~~~\alpha L= -\frac {18}{5}\frac {T}{m}\cos \theta~~~\text{(-=cw)}$$ 그리고 질량중심에서 A까지 변위를 $\vec {R}$이라면
$$ \vec {v}_A = \vec{v} + \vec {\omega} \times \vec {R} $$
$$\to~~~ \vec {a}_A = \vec{a} + \vec {\alpha}\times \vec {R} + \vec {\omega} \times ( \vec {\omega} \times \vec {R})$$
여기서 $\vec {\omega} = \frac {v_0}{L} \hat {k}$, $\vec {R}= -\frac {3L}{4} \hat {i}$, $\vec {\alpha}L = -\frac {18T\cos\theta}{5m}\hat {k}$이므로 앞의 결과를 대입하면,
$$T = \frac{10}{5+27 \cos^2 \theta} \left[\frac {3}{4 }\sin \theta + \frac {L}{D}\left(\frac{v_A}{v_0}\right)^2 \right]\frac{mv_0^2}{L}$$
'Physics > 역학' 카테고리의 다른 글
| 흔들리는 추의 각진동수는? (0) | 2025.03.13 |
|---|---|
| 떨어지지 않으려면 얼마의 속도로 줄을 당겨야 하는가? (0) | 2025.03.12 |
| 추가 원통을 감기 시작할 때 각가속도는? (0) | 2025.03.10 |
| 막대로 연결된 물체와 탄성충돌 후 속도는? (0) | 2025.03.09 |
| 충돌 후 충분한 시간이 지났을 때 운동에너지는? (0) | 2025.03.09 |




