바닥에서 구르는 원판이 그림과 같이 경사각 $\theta$인 경사면에 올라선다. 바닥과 경사면의 기하학적 구조 때문에 원판은 경사면과 충돌을 하게 되므로 질량중심이 움직이는 속도가 변하게 되고, 또 미끄러짐이 없이 경사면을 오르기 위해서는 회전각속도도 순간적으로 변해야 한다. 즉, 에너지 손실이 생기게 된다(이를 방지하기 위해서는 바닥과 경사면이 연결되는 부분을 충분히 smooth한 곡선모양으로 만들어주어야 한다) 얼마의 에너지 손실이 생길까?
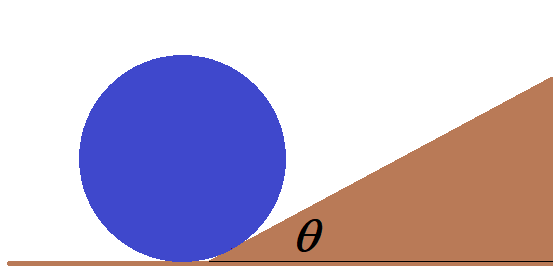

풀이: 원판은 경사면의 접촉점(두 번째 그림의 붉은 점)에서 impulsive 수직항력과 마찰력(경사면 위쪽 방향)을 받게 되므로 운동량 보존법칙을 쓸 수 없다. 그러나 이 두 impulsive force가 경사면 접촉점에 대한 토크를 만들지 않으므로 그 점에 대한 원판의 각운동량은 보존이 된다.
$$L_i = I \omega_i + mRv \cos \theta = \frac{1}{2} mRv ( 1 + 2\cos \theta) $$ $$L_f = I \omega_f + m R v_f = \frac{3}{2} mR v_f $$ 이므로 $L_f=L_i$에서 경사면을 오르기 시작하는 속도는
$$ v_f = \frac{1+ 2 \cos \theta}{3}v$$ 따라서 이 과정에서 에너지 손실은 접촉점에 대한 회전관성은 어느 지점에서나 동일하므로
$$ \eta = \frac{K_i - K_f }{K_i } = 1 - \frac{\omega _f^2}{\omega ^2}= \frac{8-4\cos \theta - 4 \cos^2 \theta}{9}$$
'Physics > 역학' 카테고리의 다른 글
| Kepler의 1 법칙(2) (1) | 2025.12.31 |
|---|---|
| Kepler의 1 법칙 (2) | 2025.12.20 |
| 회전하는 고리에서 운동하는 구슬 (0) | 2025.07.08 |
| 현수선 가장 아래에서 고리의 가속도는? (0) | 2025.03.23 |
| 줄이 팽팽해진 직후 속도는? (0) | 2025.03.16 |




