Geometry & Recognition

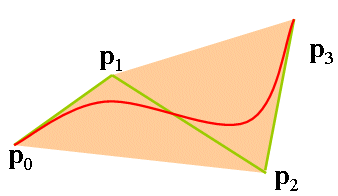
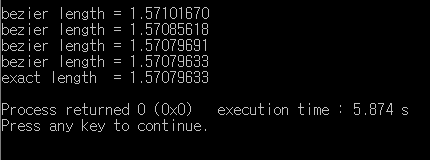
cubic Bezier 곡선은 네 개의 컨트롤 점 ($\bf {P}_0, P_1, P_2, P_3$)이용해서 표현한다:

$$\mathbf {B}(t) = (1-t)^3 \mathbf {P}_0 + 3(1-t)^2 t \mathbf {P}_1 + 3 (1-t) t^2 {\bf B}_2 + t^3 \mathbf {P}_3. \quad   0 \le t \le 1 \\{\bf B}(0) ={\bf P}_0 , ~~ {\bf B}(1) = {\bf P}_3$$

만약 곡선이 충분히 평탄하다면 굳이 삼차 다항식을 계수로 가지는 Bezier 곡선으로 표현할 필요가 없이$\mathbf {P}_0$와  ${\bf P}_3$을 잇는 직선으로 근사하는 것이 여러모로 유리할 것이다. 그러면 Bezier 곡선의 평탄성을 어떻게 예측할 것인가? 이는 cubic Bezier 곡선 ${\bf B}(t)$와 시작점과 끝점을 연결하는 직선 $\mathbf {L}(t)= (1-t) \mathbf {P}_0 + t \mathbf {P}_3$와의 차이를 비교하므로 판단할 수 있다.

직선도 cubic Bezier 곡선 표현으로 할 수 있다. 시작점이 $\mathbf {P}_0$이고 끝점이 $\mathbf {P}_3$일 때 이 둘 사이를 3 등분하는 두 내분점 $(2\mathbf {P}_0 + \mathbf{P}_3)/3$, $( \mathbf {P}_0 + 2\mathbf {P}_3)/3$을 control point에 포함시키면,

$$\mathbf {L}(t)= (1-t)^3  \mathbf {P}_0 + (1-t)^2 t (2 \mathbf {P}_0 +\mathbf {P}_3)+ (1-t) t^2  (\mathbf {P}_0 + 2 \mathbf {P}_3)+ t^3 \mathbf {P}_3$$

처럼 쓸 수 있다. Bezier 곡선과 직선의 차이를 구하면

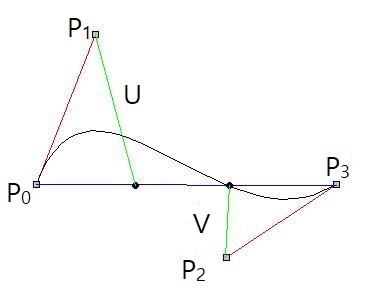
\begin{align} \Delta (t) &= |\mathbf {B}(t) - \mathbf {L}(t)| \\   &= |(1-t)^2 t (3\mathbf {P}_1 -2 \mathbf {P}_0 -\mathbf{P}_3) + (1-t) t^2(3 \mathbf {P}_2 - \mathbf {P}_0 - 2 \mathbf {P}_3)| \\ &= 3 (1-t) t |(1-t) \mathbf {U} + t \mathbf {V}|, \\ \\ &\quad \mathbf {U}=\mathbf {P}_1 - \frac{1}{3}(2 \mathbf {P}_0 + \mathbf {P}_3),   \quad \mathbf {V}=\mathbf {P}_2 - \frac{1}{3} (\mathbf {P}_0 + 2 \mathbf {P}_3)  \end{align}

그런데 

$$ \text {max} \{3(1 - t) t \} = \frac {3}{4}, \quad 0\le t \le 1, \\ \text {max}\{ |(1-t) \mathbf {U} + t \mathbf {V}| \} =\text {max}\{ |\mathbf{U}| , |\mathbf {V}|\} $$

이므로 아래와 같은 벗어난 거리의 상한 값을 얻을 수 있다:

$$ \Delta (t) \le \frac {3}{4} \text{max} \{ |\mathbf {U} | , |\mathbf {V}| \}$$

이 상한값이 주어진 임계값보다 작으면 3차 Bezier 곡선은 두 끝점을 잇는 직선으로 근사할 수 있다. 좀 더 기하학적으로 표현하면

$$|\mathbf{U}| = \mathbf{P}_1\text{에서 왼쪽 3등분 내분점까지 거리}$$

$$|\mathbf {V}|= \mathbf {P}_2 \text{에서 오른쪽 3등분 내분점까지 거리}$$

이므로,

$$ \Delta(t) \le \frac {3}{4}\times( \text{control point와 3등분 내분점 간의 거리의 최댓값}).$$

Bezier 곡선은 control points $\{ \mathbf {P}_i\}$의 선형 결합으로 주어진다:

$$\mathbf {B}(t) = \sum_{i=0}^{n} B_{ i, n} (t) \mathbf {P}_i , \quad B_{i,n}(t)=\left(\begin {array}{c} n \\ i \end {array} \right) t^i (1-t)^{n-i}.$$

Bernstein 다항식 $B_{i, n}(t)$이 control points 선형 결합의 가중치를 역할을 하는데 0과 1 사이의 양의 실수 값을 가진다. 그리고 이들 가중치의 합은 1이다:

$$ 0\le  B_{ i, n}(t) \le 1, \quad i=0,1,2,... n ,    \quad    0\le t\le 1 \\\sum_{i=0}^{n}  B_{i, n}(t) = 1$$

이는 Bezier 곡선이 control points가 만드는 convex region 내부에 있음을 의미한다. Bezier 곡선의 convexity 성질은 여러 좋은 특성을 준다.  몇 가지만 나열하면, 첫째가 Bezier 곡선은 항상 컨트롤 포인트의 convex hull 내에 놓이게 되므로 곡선의 제어 가능성을 보장한다. 둘째는 교차 여부를 쉽게 확인할 수 있다. 또한 culling을 가능하게 한다.

n 차 Bezier 곡선은 두 개의 (n - 1) 차 Bezier 곡선의 선형보간으로 표현할 수 있다. Bezier 곡선은 Bernstein 다항식을 이용해서도 표현할 수도 있지만, 높은 찻수의 곡선일 때는 De Casteljau's Algorithm을 이용하는 것이 수치적으로 보다 안정적인 결과를 준다.

// De Casteljau's algorithm; recursive version; slow for larger deg;
double Bezier(int deg, double Q[], double t) {
   if (deg == 0) return Q[0];
   else if (deg == 1) return (1-t)*Q[0] + t*Q[1];
   else if (deg == 2) return (1-t)*((1-t)*Q[0] + t*Q[1]) + t*((1-t)*Q[1] + t*Q[2]);
   else return (1 - t) * Bezier(deg-1, &Q[0], t) + t * Bezier(deg-1, &Q[1], t);
}
// De Casteljau's algorithm(degree=n-1); 
// non-recursive. Bezier() modifies Q's;
double Bezier(int deg, double Q[], double t) {
    if (deg==0) return Q[0];
    else if (deg==1) return (1-t)*Q[0] + t*Q[1];
    else if (deg==2) return (1-t)*((1-t)*Q[0] + t*Q[1]) + t*((1-t)*Q[1] + t*Q[2]);
    
    for (int k = 0; k < deg; k++)
        for (int j = 0; j < (deg - k); j++)
            Q[j] = (1 - t) * Q[j] + t * Q[j + 1];
    return Q[0];
}
void BezierCurve(std::vector<CfPt> &cntls,
                 int segments, std::vector<CfPt> &curves) {
    std::vector<double> xp(cntls.size()), yp(cntls.size());
    curves.resize(segments + 1);
    for (int i = 0; i <= segments; ++i) {
        double t = double(i) / segments;
        // clone control points; non-rec version modifies inputs;
        for (int k = cntls.size(); k-->0;) {
            xp[k] = cntls[k].x; yp[k] = cntls[k].y;
        }
        curves[i] = CfPt(Bezier(xp.size()-1, &xp[0], t), Bezier(yp.size()-1, &yp[0], t));
    }
}

곡선의 길이를 구하고자 하면 곡선을 따라 속력을 적분하면 된다. 곡선을 기술하는 벡터가 $\mathbf {B}(t) = [B_x(t), B_y(t)]$ 로 주어지면 곡선의 길이는

$$\text {Arc Length}(t_1, t_2) =\int_{t_1}^{t_2} | \mathbf {B}'(t)|dt=\int_{t_1}^{t_2} \sqrt{(B'_x(t))^2 + (B'_y(t))^2} dt.$$

그러나 일반적으로 이 적분은 닫힌 형태로 주어지지 않으므로 Gauss-Legendre quadrature와 같은 수치 적분에 의존해서 그 값을 계산하여야 한다.
Bezier curve의 경우는 기하학적인 방법을 이용하여서 좀 더 간편하게 그 길이를 구할 수 있다. Bezier curve의 길이에 대한 간단한 근사는 현의 길이($|\mathbf{Q}_3- \mathbf {Q}_0|$)로 근사하는 것이다. 그러나 현의 길이는 lower bound만을 준다. 다음으로 고려할 근사는  control 점 사이 거리의 합이다. 이것은 실제 길이의 upper bound를 준다. 따라서 근사적인 길이는 이 두 거리의 평균으로 잡으면 될 것이다:

$$ \text{Arc Length}\sim \frac{ \text {cord length} + \sum\text {distance between control points}}{2}.$$

그러나 이 근사가 유효하기 위해서는 현의 길이와 control point 간의 거리의 합

$$|\mathbf{Q}_3- \mathbf {Q}_2|+ |\mathbf {Q}_2- \mathbf {Q}_1| +|\mathbf {Q}_1- \mathbf {Q}_0|$$

의 차이가 충분히 작아야 한다. 만약에 이 두 길이의 차이기 정해진 임계값보다도 크면 Bezier curve를 둘로 분할해서 좌우 두 Bezier curve에 대해서 동일한 검사를 한다. 충분히 평탄한 경우는 위의 평균값으로 근사하고 그렇지 못한 경우는 충분히 평탄해질 때까지 분할하는 과정을 반복한다. 아래 코드는 3차 Bezier curve의 길이를 이 알고리즘을 이용해서 구하는 과정을 구현한 것이다.

#define DistL2(A, B) sqrt(((A).x-(B).x)*((A).x-(B).x) + ((A).y-(B).y)*((A).y-(B).y))
static void BezierSubDiv(CfPt Q[4], CfPt leftQ[4], CfPt rightQ[4]) {
    CfPt T[4][4];                      /* Triangle Matrix */
    for (int j = 0; j < 4; ++j) T[0][j] = Q[j];
    // de Casteljau divides and conquers at t = 0.5;
    for (int i = 1; i < 4; ++i)
        for (int j = 0 ; j <= 3 - i; ++j)
            T[i][j] = (T[i - 1][j] + T[i - 1][j + 1]) / 2;
            
    // left subdiv control points;
    for (int j = 0; j < 4; ++j) leftQ[j]  = T[j][0];
    // right subdiv control points;
    for (int j = 0; j < 4; ++j) rightQ[j] = T[3 - j][j];
}                                        
void BezierLength(CfPt Q[4], double tol, double *length) {
    CfPt leftQ[4], rightQ[4];                
    double controlLen = 0;  
    for (int i = 0; i < 3; ++i) controlLen += DistL2(Q[i], Q[i + 1]);
    double cordLen = DistL2(Q[0], Q[3]);
    // test flatness;
    if (fabs(controlLen - cordLen) > tol) {
        BezierSubDiv(Q, leftQ, rightQ);              /* divide */
        BezierLength(leftQ, tol, length);            /* left side */
        BezierLength(rightQ, tol, length);           /* right side */
        return;
    }
    *length = *length + (cordLen + controlLen) / 2 ;
    return ;
}

다음은 4분원의 길이를 위의 알고리즘을 이용해서 구하는 예제이다. 네 개의 control point는

$$ Q_1=(0,1), ~~Q_2 = (k, 1),~~Q_3=(1, k),~~Q_4=(1,0)$$

이고, $k$ 값은 Bezier curve의 중간이 원에 접하는 경우, 원과 벗어남이 가장 작은 경우, 면적을 같게 하는 경우, 길이를 같게 하는 경우 각각에 대해 계산을 한다. 

int main() {
    double k[4] = {0.5522847498, //touch at t = 0.5;
                   0.551915023,  //min-deviation;
                   0.551778477,  //match area;
                   0.551777131   //match length;
                   };
    for (int i = 0; i < 4; i++)
        printf("bezier length = %.8f\n", BezierLengthCircle(k[i]));
    printf("exact length  = %.8f\n", 2.0 * atan(1.));
    return 0;
}
double BezierLengthCircle(double k) {
    CfPt Q[4] = {{0, 1.}, {k, 1.}, {1., k}, {1., 0.}};
    double len = 0;
    double tol = 1.e-20;//
    BezierLength(Q, tol, &len);
    return len;
};

Bezier 곡선을 이용한 원의 근사처럼 타원을 근사해보도록 하자. 원점을 중심으로 하고 장축 반지름이 $a$, 단축 반지름이 $b$인 타원을 1사분에서 3차 Bezier curve을 이용해서 근사하려면 4개의 control point가 필요하다. 원의 경우처럼, 끝점에서 접선의 기울기를 같게 하는 조건을 부여하면 control point는 

$$\mathbf {P_0} = (0, b), \quad \mathbf {P}_1 = (ka, b), \quad \mathbf {P}_2 =( a, kb),\quad \mathbf {P}_3 = (a, 0)$$

로 잡을 수 있다. 따라서

$$\mathbf {B}(t) = (1-t^3) \mathbf {P}_0 + 3t(1-t)^2 \mathbf {P}_1 + 3t^2 (1-t) \mathbf {P}_2 + t^3 \mathbf {P}_3 = \left(\begin {array}{c} a x(t) \\ b y(t) \end {array}\right) $$

$$ x(t) = 3k (1-t)^2 t + 3 (1-t) t^2 + t^3 \\ y(t) = 3k t^2 (1-t) + 3t(1-t)^2 + (1-t)^3 $$

$t=1/2$일 때 $(a/\sqrt {2}, b/\sqrt {2})$을 통과하는 조건을 부여하면, 원과 마찬가지로

$$ k = \frac {4}{3}(\sqrt {2}-1)= 0.5522847498...$$

을 얻는다. Mahalanobis measure를 기준으로 거리를 측정하면  타원의 경우도 벗어남 에러가

$$ \Delta (t) = \sqrt { \frac {B_x^2(t)}{a^2} + \frac {B_y^2(t)}{b^2} }  -1 =\sqrt {x^2(t)+y^2(t)}-1$$

원의 경우와 같음을 쉽게 알 수 있다.

회전된 타원; 

2사분면: $(x, y) \rightarrow (-x, y)$

3사분면: $(x, y) \rightarrow (-x, -y)$

4사분면: $(x, y) \rightarrow (x, -y)$

void BezierEllipse(CDC *pDC, CPoint center, double a, double b) {
    const double k = 0.5522847498;
    CPen red(PS_SOLID, 3, RGB(0xFF, 0, 0));
    CPen *pOld = pDC->SelectObject(&red);
    CPoint P[4];  //control pts;
    P[0] = CPoint(center.x,                    int(center.y - b + 0.5));
    P[1] = CPoint(int(center.x + k * a + 0.5), int(center.y - b + 0.5));
    P[2] = CPoint(int(center.x + a + 0.5),     int(center.y - k * b + 0.5));
    P[3] = CPoint(int(center.x + a + 0.5),     center.y);
    pDC->PolyBezier(P, 4);
    pDC->SelectObject(pOld);
}

void BezierEllipse(CDC *pDC, CPoint center, double a, double b, double ang) {
    const double k = 0.5522847498;
    const double cosang = cos(ang);
    const double sinang = sin(ang);
    CPoint P[4];
    double x[4], y[4], xt[4], yt[4];
    //1사분면: 
    x[0] = 0,     y[0] = b;
    x[1] = k * a, y[1] = b;
    x[2] = a,     y[2] = k * b;
    x[3] = a,     y[3] = 0;
    CPen red(PS_SOLID, 3, RGB(0xFF, 0, 0));
    CPen *pOld = pDC->SelectObject(&red);    
    for (int i = 0; i < 4; i++) {
        xt[i] = x[i] * cosang - y[i] * sinang;
        yt[i] = x[i] * sinang + y[i] * cosang;
        P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
    }
    pDC->PolyBezier(P, 4);
    pDC->SelectObject(pOld);
    //4사분면;(x, -y);
    CPen blue(PS_SOLID, 3, RGB(0, 0, 0xFF));
    pOld = pDC->SelectObject(&blue);
    for (int i = 0; i < 4; i++) {
        xt[i] = x[i] * cosang - (-y[i]) * sinang;
        yt[i] = x[i] * sinang + (-y[i]) * cosang;
        P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
    }
    pDC->PolyBezier(P, 4);
    pDC->SelectObject(pOld);
    //3-사분면;(-x,-y)
    CPen green(PS_SOLID, 3, RGB(0, 0xFF, 0));
    pOld = pDC->SelectObject(&green);
    for (int i = 0; i < 4; i++) {
        xt[i] = (-x[i]) * cosang - (-y[i]) * sinang;
        yt[i] = (-x[i]) * sinang + (-y[i]) * cosang;
        P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
    }
    pDC->PolyBezier(P, 4);
    pDC->SelectObject(pOld);
    //2사분면;(-x,y);    
    CPen magenta(PS_SOLID, 3, RGB(0xFF, 0, 0xFF));
    pOld = pDC->SelectObject(&magenta);
    for (int i = 0; i < 4; i++) {
        xt[i] = (-x[i]) * cosang - y[i] * sinang;
        yt[i] = (-x[i]) * sinang + y[i] * cosang;
        P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
    }
    pDC->PolyBezier(P, 4);
    pDC->SelectObject(pOld);
}