$$ I = \int_0^\infty \frac{\log(1+x^2) dx} { 1+x^2} = \pi\log2$$
함수 $$f(z) = \frac{\log(i + z)}{1+z^2}$$을 그림과 같은 경로에서 적분을 하자.
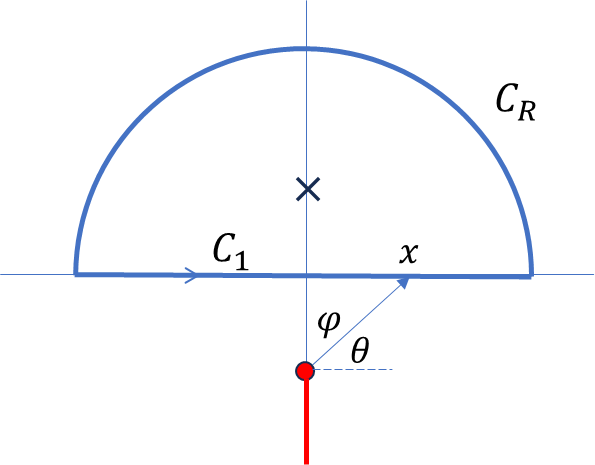
Branch cut은 음의 허수축이고, $-\frac{\pi}{2}\le \arg(i+z)\le \frac{3\pi}{2}$. $z=i$가 $f(z)$의 simple pole이고, residue는
$$ \text{ Res} f(i) = \frac{\log(2e^{i\pi/2})}{ 2i} = \frac{\log(2) + i \frac{\pi}{2}}{2i} = \frac{1}{2i} \log(2) + \frac{\pi}{4}$$
$C_1$에서 $z=x$, $z+i=\sqrt{1+x^2} e^{i \theta}, ~\tan\theta=1/x$이므로
$$\int_{C_1} f(z) dz = \int_{-\infty}^{\infty} \frac{ \frac{1}{2}\log(1+x^2) + i \theta}{1+x^2 } dx= I + i \int_{-\infty}^\infty \frac{\theta}{1+x^2} dx$$
이 적분의 허수부는 $\tan \varphi = x ~(-\frac{\pi}{2}\le \varphi\le \frac{\pi}{2})$로 치환을 하면 $$\theta = \frac{\pi}{2} - \varphi \\ \int_{-\infty}^\infty \frac{\theta}{1+x^2}dx = \int_{-\pi/2}^{\pi/2} \theta d \varphi = \frac{\pi^2}{2}$$
그리고 $C_R: ~z=Re^{i \theta}$에서는 $$ \int_{C_R} \sim \frac{\log(R)}{R}\to 0$$이므로 기여가 없다. 따라서 Residue 정리에 의해 $$\oint f(z)dz=2\pi \times \text{Res}f(i) \\\to ~ I + i \frac{\pi^2}{2} = 2\pi i \times \text{Res}f(i) = \pi \log(2) + i \frac{\pi^2}{2}$$
허수부는 항등적으로 만족하고, 실수부에서
$$ I = \pi \log(2) $$
임을 알 수 있다.
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-036 (0) | 2024.11.20 |
|---|---|
| Integration along a branch cut-035 (0) | 2024.11.19 |
| Integrate [log(1+x)/(1+x^2), {x, 0, 1}] (0) | 2024.11.15 |
| Integrate [log(1+x)/x, {x, -1, 1}] (0) | 2024.11.13 |
| Integration along a branch cut-034 (0) | 2024.11.10 |




