Geometry & Recognition

사람이 걷는 동작은 복잡하지만 몇 가지 가정을 하면 단순한 강체의 운동으로 근사를 할 수 있다. 우선 사람이 걷는 동안 항상 한 발은 땅을 딛고 있다. 그리고 땅을 딛고 있는 발을 기준으로 몸의 질량중심은 원호를 그리면서 거의 일정한 속도로 움직이게 된다. 사람을 질량중심에 모든 질량이 뭉친 점으로 근사를 하면 걷는 동작은 거의 질량이 없는 막대(다리: 길이=$L$)에 매달린 역진자(inverted pendulum) 운동과 비슷하다고 볼 수 있다. 또한 원호를 따라 중심이 이동하는 속력은 거의 일정하다고 근사할 수 있다.

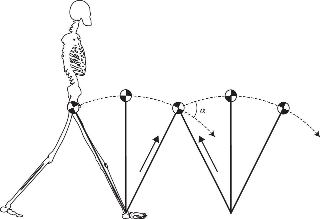
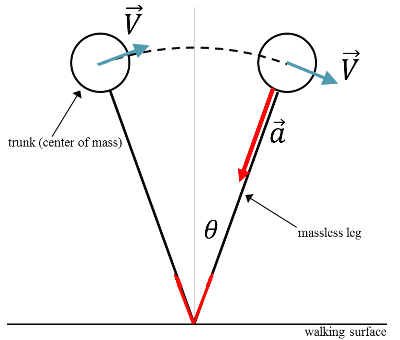
이 경우에 질량중심은 등속 원운동을 한다고 볼 수 있고, 뉴턴의 제2법칙에 의해서 질량중심에서 발 쪽을 향하는 힘 성분이 구심력 역할을 한다. 구심력 역학을 할 수 있는 힘은 중력, 수직항력, 그리고 마찰력이 있다.

수직에서 $\theta$만큼 기울어졌을 때 등속원운동의 가속도 벡터는

$$ \vec{a} =\frac{V^2}{L} (-\sin \theta \hat{x} -\cos \theta \hat{y})$$

이고,  운동 방정식의 수식 성분을 보면 중력과 수직항력이 기여하므로

$$ \sum F_y = N - mg = m a_y = -\frac{m V^2}{L} \cos \theta $$

움직이는 속력이 너무 빠르면 달리는 동작이 되고, 이 경우 양발이 땅에서 떨어지게 된다. 발이 땅에서 떨어지지 않으려면  수직항력 $N\ge0$인 조건을 만족하도록 걷는 속력을 조절해야 한다. 

$$N \ge  0 \quad \rightarrow  \quad V \le  \sqrt{\frac{gL }{\cos \theta}}$$

원호를 그리며 움직이는 동안 이 관계가 성립해야 하므로 걷기가 가능한 최대속력은:

$$V_\text{max} = \sqrt{gL}$$

사람을 너무 단순화시킨 감은 있지만 왜 다리가 긴 사람이 더 빨리 걸을 수 있는지를 물리 법칙으로 추정할 수 있다는 것을 보여준다. 사람을 좀 더 복잡한 강체로 근사하더라도 $\sqrt{gL}$ 앞의 factor만 바뀔 것이다.  사람이 걷는 동안 땅을 딛지 않는 발은 약간 구부러진 상태로 엉덩이를 축으로 일종의 물리진자처럼 행동하는데 이를 이용해도 역시 같은 추정치를 얻을 수 있다.

다리 길이가 $L=1\text{m}$이면,  $V_\text{max}= \sqrt{(1 \text{m}) \times (9.8\text{m/s}^2)} = 3.13\text{m/s}=11.3\text{km/h}$. 경보 세계기록이 대략 $15\text{km/h}$이므로 합리적인 추정이 된다.

youtu.be/HypJY1XWkWY

책상에 세워둔 연필이 넘어져서 바닥에 닿는데 걸리는 시간은 어떻게 될까? 대략 경험적으로 보면 연필 길이가 길수록 넘어지는데 시간이 오래 걸린다. 왜 그럴까? 넘어지는데 걸리는 시간은 연필의 운동을 결정하는 물리량과 관련 있는데, 우선 크기와 관련 있는 길이$(L)$가 있고, 넘어지려면 토크를 작용해야 하는데 이는 중력(가속도: $g$)과 관련이 있다.(마찰/수직 항력은 회전축에 걸리므로 무관하다). 물론 질량에도 의존할 수 있는데, 중력 가속도, 길이, 질량의 물리량으로 시간의 단위를 만들 수 있는 조합은 $\text{const} \times\sqrt { L /g}$ 밖에 없다. 즉, 넘어지는데 걸리는 시간은 길이에 제곱근에 비례한다. 

구체적으로 얼마나 걸리는지 계산을 시도해 보자. 연필이 넘어지면 수직과 이루는 각 $\theta$가 증가한다: $0\rightarrow \pi/2$. 뉴턴 방정식을 이용하면 $\theta$가 만족해야 할 미분방정식을 얻을 수 있지만, 실질적으로 일하는 힘이 중력밖에 없으므로 역학적 에너지가 보존된다는 사실을 이용하는 것이 좀 더 수월하다. 연필을 균일한 막대로 근사하면 넘어지는 과정은 연필심에 대한 회전운동이다. 역학적 에너지 보존식을 쓰면

$$\frac {1}{2} I_{tip} \Big(\frac {d\theta}{dt}\Big)^2 + \frac {1}{2} MgL \cos \theta = \text {const} = \frac {1}{2} MgL.$$ 여기서 각속도를 구하면

$$ \\ \frac{d\theta}{dt} = \sqrt { \frac {3g}{L}  (1- \cos \theta ) } = \sqrt {\frac {6g}{L}} \sin \frac {\theta}{2},$$

이고, 적분하여 수직 상태에서 바닥에 도달하는데 걸리는 시간을 구하면,

$$T= \sqrt { \frac {L}{6g}} \int_0^{\pi/2} \frac {d \theta }{\sin \frac {\theta}{2} } \rightarrow \infty.$$

기대(?)와는 다르지만 이 결과는 구체적으로 계산하지 않더라도 예상할 수 있다. 왜냐면 완전히 똑바로 서 있으면 회전의 시작에 필요한 토크를 생성하는 힘이 없기 때문이다. 연필에는 중력이 작용하고 끝에 마찰력이나 수직 항력이 있긴 하지만 토크를 만들지는 못한다. 따라서 연필을 넘어뜨리기 위해서는 처음에 약간의 충격을 주던지(속도 제공) 아니면 약간 기울인 상태에서 시작해야 한다. 처음 $\theta_0$의 각도에서 시작하였다면 걸리는 시간은 위 적분식에서

$$ T = \sqrt{\frac {2L}{3g} }\log \frac { \tan \frac {\pi}{8}}{\tan \frac {\theta_0}{4} }.$$

$\theta_0\rightarrow 0$이면 시간은 $T\sim -\sqrt { \frac {2L}{3g}} \log \theta_0 \rightarrow \infty$이고, 유한할 때는 길이의 제곱근에 비례함도 확인할 수 있다.

youtu.be/oowAdPjDY5M

야구 배트로 공을 칠 때 공을 맞추는 지점을 잘 선택하면 배트를 잡는 위치(회전축)의 움직임이 거의 없게(즉, 손이 충격을 안 받게) 만들 수 있다. 이는 배트가 힘을 받았을 때 운동이 질량중심과 같은 속도로 움직이는 병진 운동과 질량중심에 대한 회전운동의 합으로 표현되는 점을 고려하면 쉽게 이해할 수 있다. 배트의 각 지점의 실제 속도는 질량중심의 속도와 회전운동에 의한 속도의 벡터 합이므로 손잡이 부분에서 0인 조건을 만족되면 가능하게 된다. 이 경우 배트의 운동은 손잡이 위치에 대한 순수 회전운동으로 표현할 수 있다. 그리고 공을 맞추는 지점을 center of percussion(COP)이라고 한다(손잡이 위치에 대한 상대적 위치임)

공이 배트에 준 힘을 $F$라면 (손이 준 힘이 없는 조건에서)

$$\text {cm-병진}:  ~F = M a,$$

$$\text {cm-회전}: ~Fb = I_{cm} \alpha. $$

손잡이 지점의 가속도가 없는 조건을 쓰면(질량중심 가속도+ 질량중심에 대한 회전운동의 접선가속도)

$$ a_{손잡이}= a- \alpha p = 0\quad \rightarrow ~ \frac {F}{M} = \frac {Fb} {I_{cm}} p \quad \therefore b =  \frac {I_{cm}}{pM}.$$ 예를 들면 방망이가 길이가 $L$인 단순막대의 끝을 잡고 휘두르는 경우, $p = L/2$, $I_{cm} = ML^2/12$이므로 $b=L/6$임을 알 수 있다. 또 $b$와 $p$는 정확히 대칭적 역할을 한다. 배트의 COP 지점을 손으로 잡고 원래 손잡이 위치에 공을 맞추어도 손에 충격이 오지 않는다.

배트의 회전관성을 직접 구하지 않고 COP을 알아낼 수 있는 방법은 없을까? 배트의 손잡이를 회전축으로 만들어 배트를 살짝 흔들면 주기가 일정한 진동 운동을 한다(물리진자, COP를 회전축으로 만들어도 같은 주기를 가진다). 그리고 주기는 다음과 같이 주어진다: 

$$ T ={2\pi} \sqrt{ \frac{I_{cm} + M p^2 }{ Mgp}} = 2\pi \sqrt{\frac{b+p}{g}} .$$  

이 표현은 길이가 $\ell=b+p$인 단순진자의 주기와 같다. 따라서 단순진자의 길이를 바꾸어 가면서 배트와 같은 주기를 같게 되는 경우를 찾으면  $b+p$ 값을 구할 수 있다. (추가로 배트의 질량중심은 균형을 이용하면 쉽게 찾을 수 있다.)

https://youtu.be/Dw3UpKQVhVY