Bezier 곡선을 이용한 원의 근사처럼 타원을 근사해보도록 하자. 원점을 중심으로 하고 장축 반지름이 $a$, 단축 반지름이 $b$인 타원을 1사분에서 3차 Bezier curve을 이용해서 근사하려면 4개의 control point가 필요하다. 원의 경우처럼, 끝점에서 접선의 기울기를 같게 하는 조건을 부여하면 control point는
$$\mathbf {P_0} = (0, b), \quad \mathbf {P}_1 = (ka, b), \quad \mathbf {P}_2 =( a, kb),\quad \mathbf {P}_3 = (a, 0)$$
로 잡을 수 있다. 따라서
$$\mathbf {B}(t) = (1-t^3) \mathbf {P}_0 + 3t(1-t)^2 \mathbf {P}_1 + 3t^2 (1-t) \mathbf {P}_2 + t^3 \mathbf {P}_3 = \left(\begin {array}{c} a x(t) \\ b y(t) \end {array}\right) $$
$$ x(t) = 3k (1-t)^2 t + 3 (1-t) t^2 + t^3 $$
$$ y(t) = 3k t^2 (1-t) + 3t(1-t)^2 + (1-t)^3 $$
$t=1/2$일 때 $(a/\sqrt {2}, b/\sqrt {2})$을 통과하는 조건을 부여하면, 원과 마찬가지로
$$ k = \frac {4}{3}(\sqrt {2}-1)= 0.5522847498...$$
을 얻는다. Mahalanobis measure를 기준으로 거리를 측정하면 타원의 경우도 벗어남 에러가
$$ \Delta (t) = \sqrt { \frac {B_x^2(t)}{a^2} + \frac {B_y^2(t)}{b^2} } -1 =\sqrt {x^2(t)+y^2(t)}-1$$
원의 경우와 같음을 쉽게 알 수 있다.
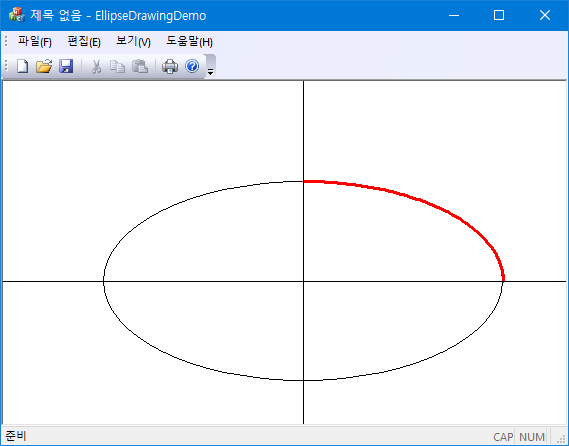
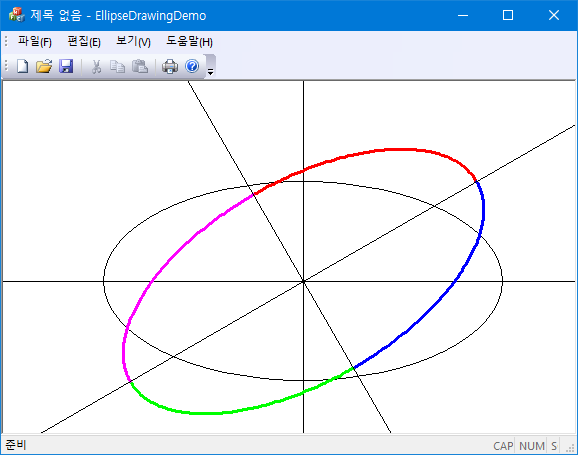
회전된 타원;
2사분면: $(x, y) \rightarrow (-x, y)$
3사분면: $(x, y) \rightarrow (-x, -y)$
4사분면: $(x, y) \rightarrow (x, -y)$
void BezierEllipse(CDC *pDC, CPoint center, double a, double b) {
const double k = 0.5522847498;
CPen red(PS_SOLID, 3, RGB(0xFF, 0, 0));
CPen *pOld = pDC->SelectObject(&red);
CPoint P[4]; //control pts;
P[0] = CPoint(center.x, int(center.y - b + 0.5));
P[1] = CPoint(int(center.x + k * a + 0.5), int(center.y - b + 0.5));
P[2] = CPoint(int(center.x + a + 0.5), int(center.y - k * b + 0.5));
P[3] = CPoint(int(center.x + a + 0.5), center.y);
pDC->PolyBezier(P, 4);
pDC->SelectObject(pOld);
}void BezierEllipse(CDC *pDC, CPoint center, double a, double b, double ang) {
const double k = 0.5522847498;
const double cosang = cos(ang);
const double sinang = sin(ang);
CPoint P[4];
double x[4], y[4], xt[4], yt[4];
//1사분면:
x[0] = 0, y[0] = b;
x[1] = k * a, y[1] = b;
x[2] = a, y[2] = k * b;
x[3] = a, y[3] = 0;
CPen red(PS_SOLID, 3, RGB(0xFF, 0, 0));
CPen *pOld = pDC->SelectObject(&red);
for (int i = 0; i < 4; i++) {
xt[i] = x[i] * cosang - y[i] * sinang;
yt[i] = x[i] * sinang + y[i] * cosang;
P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
}
pDC->PolyBezier(P, 4);
pDC->SelectObject(pOld);
//4사분면;(x, -y);
CPen blue(PS_SOLID, 3, RGB(0, 0, 0xFF));
pOld = pDC->SelectObject(&blue);
for (int i = 0; i < 4; i++) {
xt[i] = x[i] * cosang - (-y[i]) * sinang;
yt[i] = x[i] * sinang + (-y[i]) * cosang;
P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
}
pDC->PolyBezier(P, 4);
pDC->SelectObject(pOld);
//3-사분면;(-x,-y)
CPen green(PS_SOLID, 3, RGB(0, 0xFF, 0));
pOld = pDC->SelectObject(&green);
for (int i = 0; i < 4; i++) {
xt[i] = (-x[i]) * cosang - (-y[i]) * sinang;
yt[i] = (-x[i]) * sinang + (-y[i]) * cosang;
P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
}
pDC->PolyBezier(P, 4);
pDC->SelectObject(pOld);
//2사분면;(-x,y);
CPen magenta(PS_SOLID, 3, RGB(0xFF, 0, 0xFF));
pOld = pDC->SelectObject(&magenta);
for (int i = 0; i < 4; i++) {
xt[i] = (-x[i]) * cosang - y[i] * sinang;
yt[i] = (-x[i]) * sinang + y[i] * cosang;
P[i] = CPoint(int(center.x + xt[i] + 0.5), int(center.y - yt[i] + 0.5));
}
pDC->PolyBezier(P, 4);
pDC->SelectObject(pOld);
}'Computational Geometry' 카테고리의 다른 글
| De Casteljau's Algorithm (0) | 2021.04.22 |
|---|---|
| Arc Length of Bezier Curves (0) | 2021.04.21 |
| Bezier Curve Approximation of a Circle (0) | 2021.04.10 |
| Bresenham's Line Algorithm (0) | 2021.04.07 |
| Rotating Calipers (3) | 2021.03.31 |




