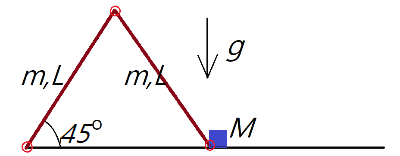
그림처럼 경첩으로 연결된 동일한 두 막대가 있다. 왼쪽 막대는 바닥 경첩에, 오른쪽 막대는 질량 $M$인 물체에 경첩으로 연결되어 있다. 두 막대의 중간 연결 부위가 바닥에 닿는 속도는 $\sqrt{gL}$의 몇 배인가? 마찰은 없다.
1. $\sqrt{\frac{3\sqrt{2}}{2}}$
2. $\sqrt{\frac{3\sqrt{2}}{2}}$ 보다 크다.
3. $\sqrt{\frac{3\sqrt{2}}{2}}$ 보다 작다.
더보기
중간 부분이 바닥에 닿는 순간 $M$은 정지하고, 두 막대는 같은 각속도를 가진다. 왼쪽 막대는 시계방향, 오른쪽 막대는 순간적으로 $M$을 기준으로 같은 각속도를 회전한다(순간 회전축). 역학적 에너지 보존을 적용하면,
$$ 2\times mg\frac{L}{2} \sin(45^\circ) = \frac{1}{2} I \omega^2 \times 2 \quad \rightarrow ~~\therefore \omega=\sqrt{\frac{3\sqrt{2}g}{2L}}$$
$$\therefore ~v=\sqrt{\frac{3\sqrt{2}gL}{2}}$$
728x90
'Physics > 역학' 카테고리의 다른 글
| 마찰계수는? (0) | 2022.02.20 |
|---|---|
| 경사면의 가속도는? (0) | 2022.02.20 |
| 어디에 도착하는가? (0) | 2022.02.19 |
| 적도에서 출발한 미사일이 북극에 도달하려면? (0) | 2022.02.16 |
| 지구의 반쪽끼리 서로 당기는 중력의 세기는? (0) | 2022.02.16 |



