Fourier Series를 이용한 Isoperimetric Inequality 증명

면적이 $A$인 단순 평면 도형이 있을 때 그 둘레의 길이 $L$과의 사이에는 다음 부등식이 성립한다:

$$L^2\ge 4\pi A$$

정 $n$ 각형에 대해서 이 부등식을 체크해 보면

$$\frac{L^2}{4\pi A}=\frac{\tan (\pi /n)}{\pi /n}=\{\begin{array}{cc}1.654& \text{정삼각형}\\ 1.273& \text{정사각형}\\ 1.156& \text{정오각형}\\ 1.034& \text{정십각형}\end{array}$$

증명: 평면에서 둘레의 길이가 $L$인 한 폐곡선을 곡선을 따라 움직인 길이를 매개변수로 사용해서 표현하자: $(x(s),y(s)),s\in [0,L]$. 이 폐곡선을 복소평면으로 옮기면 $z(s)=x(s)+iy(s)$로 표시할 수 있다. $z(s)$는 $s$에 대해서 주기가 $L$ 복소함수로 볼 수 있다. Fourier series를 사용하기 편리하게 하기 위해서 매개변수를 바꿔 $z(t)=x(Lt/2\pi )+iy(Lt/2\pi )$로 표현하자. 그러면 $t$에 대한 주기가 $2\pi$가 되고 다음과 같이 Fourier 전개를 쓸 수 있다. (영상처리에서는 물체의 윤곽선에 대한 Fourier  계수를 이용해서 물체의 모양을 분류하는데 이용이 된다)

$$z(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_k{e}^{ikt}$$

먼저 $L^2$항을 뽑아내기 위해 다음의 적분을 고려하자. $s=Lt/2\pi$로 놓으면 $z(s)$은 곡선의 길이를 매개변수로 사용한 것이어서  $|dz/ds|=1$이므로

$${\int }_0^{2\pi }{\left|\frac{dz}{dt}\right|}^{2}dt={\int }_0^{2\pi }{\left|\frac{dz}{ds}\right|}^2{\left(\frac{ds}{dt}\right)}^{2}dt=\frac{L^2}{4{\pi }^2}{\int }_0^{2\pi }dt=\frac{L^2}{2\pi }$$ 

좌변에 Fourier 전개를 대입하면 (note: ${\int }_0^{2\pi }{e}^{i(k-j)t}dt=2\pi {\delta }_{kj}$)

$$\begin{array}{r}{\int }_0^{2\pi }{\left|\frac{dz}{dt}\right|}^{2}dt=2\pi \sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{k}^2|a_k{|}^2\end{array}$$

을 얻는다. 따라서

$$\frac{L^2}{4{\pi }^2}=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{k}^2|a_k{|}^2$$

다음으로 도형의 면적으로 표현하자.

$$\begin{array}{rl}A& =\frac{1}{2}{\int }_0^{2\pi }(x\frac{dy}{dt}-y\frac{dx}{dt})dt\\ & =\frac{1}{2}\text{Re}{\int }_0^{2\pi }iz\overline{\frac{dz}{dt}}dt=\pi \sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}k|a_k{|}^2\end{array}$$

그런데 $$\sum _k{k}^2|a_k{|}^2\ge \sum _{k}k|a_k{|}^2$$

이므로

$$\frac{L^2}{4\pi }\ge A$$

을 얻는다. 그리고 등호 성립하려면 Fourier 계수가 $k=0,1$이외에는 모두 0이어야 된다. 즉

$$z(t)=a_0+a_1{e}^{it}$$

인 경우인데, 이는 복소평면에서  중심이 $a_0$, 반지름이 $|a_1|$인 원을 나타낸다.

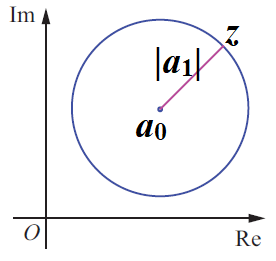
변분법을 이용해서도 원이 주어진 둘레길이를 가지는 평면도형 중에서 가장 넓은 면적의 도형임을 쉽게 보일 수 있다. 

https://kipl.tistory.com/187

주어진 길이의 폐곡선으로 가둘 수 있는 최대 면적의 도형은?