수직 평면 상에서 곡선 $y=y(x)$을 따라 움직이는 물체의 운동을 생각하자. 이 물체는 마찰이 없이 움직일 수 있고 일정한 중력의 영향을 받는다. 높이 $y=h$에서 출발하여 바닥 $y=0$에 도달하는 데 걸리는 시간은 일반적으로 출발 높이에 따라 달라진다. 역학적 에너지 보존법칙을 쓰면 바닥까지 내려오는 데 걸리는 시간 $T(h)$는
$$ \frac{1}{2} \Big(\frac{d\ell}{dt}\Big)^2 + mgy = mgh \quad \Longrightarrow \quad T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{d \ell }{\sqrt{h-y}}$$
일반적으로 출발 높이가 낮으면 움직이는 거리가 짧아지므로 도착 시간도 짧아진다. 그러나 가속이 충분히 되지 않으므로 거리에 비례해서 시간이 짧아지지는 않는다. 그럼 도착 시간이 출발 높이에 무관하게 일정한 곡선을 찾을 수 있을까? 물론 답은 있고, 그때 물체가 움직이는 곡선을 tautochrone curve(등시곡선)이라 부른다.
물체가 움직이는 경로의 line element $d\ell $를 $$ d\ell = \sqrt{dx^2 +dy^2} = \sqrt{ 1 + \Big(\frac{dx}{dy}\Big)^2 } dy= f(y)dy$$처럼 쓰면 도착 시간은 $$T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{f(y)}{\sqrt{h-y}} dy$$
가 된다. 이는 $f(y)$와 $1/\sqrt{y}$의 convolution 형태가 되어 Laplace 변환을 사용하기 좋은 모양이다. 양변에 Laplace 변환을 취하면
\begin{align} \widetilde{T}(s) &= \frac{1}{\sqrt{2g}} \int_0^\infty \int_0^h \frac{f(y)}{\sqrt{h-y}} e^{-sh} dy dh\\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s){ \cal L}\Big[\frac{1}{\sqrt{h}}\Big](s) \\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s) \sqrt{\frac{\pi}{s}} \end{align} 여기서 $ { \cal L}\left[\frac{1}{\sqrt{h}} \right] =\sqrt{\frac{\pi}{s}}$임을 이용했다 $\left(\int_0^\infty \frac{e^{-sh}}{\sqrt{h}}dh = 2 \int_0^\infty {e^{-st^2}}dt = \sqrt{\frac{\pi}{s}}\right)$.
도착 시간이 높이에 무관하게 일정하다면 $$T(h)= T_0=\text{const}$$로 쓸 수 있으므로 Laplace 변환은 $\widetilde{T}(s) = T_0/s$이다. 따라서 곡선 형태를 결정하는 $f(y)$의 Laplace 변환은
$$ \tilde{f}(s) = \sqrt{\frac{2gT_0^2}{\pi^2}} \sqrt{\frac{\pi}{s}}$$ 이를 역변환시키면
$$ f(y) = \sqrt{\frac{2gT_0^2}{\pi^2}} \frac{1}{\sqrt{y}} $$임을 쉽게 알 수 있다. 이제 구체적인 곡선의 형태를 구하면 $$ x=\int dx =\int \sqrt{f^2(y)-1} dy =\int \sqrt{ \frac{{2gT_0^2}/{\pi^2 } - y}{y}}dy$$이고, 적분하기 위해 곡선이 $(x,y)=(0,0)$을 통과하는 조건을 주자. 그리고 $$y = \frac{2gT_0^2}{\pi^2} \sin ^2( \theta/2) = \frac{gT_0^2}{\pi^2} (1- \cos \theta)$$로 매개변수화하면(이 경우 $dy/dx = \tan (\theta/2)$)
$$ x = \int_0^{ \theta_0} \frac{ gT_0^2}{\pi^2} (1 +\cos \theta) d \theta \quad \Longrightarrow \quad x = \frac{gT_0^2}{\pi^2}( \theta + \sin \theta)$$
이어서 $(x(\theta), y(\theta))$는 cycloid가 됨을 알 수 있다. 이 cycloid는 반지름 $gT_0^2/\pi^2$인 원을 일정한 높이의 수평선 $y=2gT_0^2/\pi^2$에 접하게 굴릴 때 원점에서 바닥과 접촉했던 점이 그리는 곡선이고, $\theta$는 원의 중심과 이 점을 잇는 선분이 수직과 이루는 각을 나타낸다.
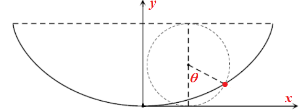
위에서 구한 cycloid 곡선을 도착시간 공식에 대입해서 확인해 보자. 출발 높이가 $h$일 때 $h = \frac{gT_0^2}{\pi^2}( 1- \cos \theta_0)$로 놓으면 $$h-y= \frac{gT_0^2}{\pi^2} (\cos \theta - \cos \theta_0) \\ d\ell = \frac{gT_0^2 }{\pi^2}\sqrt{2(1+\cos \theta) } d \theta $$
이므로 내려가는데 걸리는 시간 \begin{align} T(h) & = \frac{T_0}{\pi} \int_0^{\theta_0} \sqrt{ \frac{1+\cos \theta}{ \cos \theta - \cos \theta_0 }} d \theta \\ &= \frac{2T_0}{\pi} \int_0^{\theta_0} {\frac{d\sin (\theta/2)}{\sqrt{\sin^2(\theta_0/2)-\sin^2(\theta/2)}}}= T_0 \end{align}이 출발 높이($=h$)에 상관없이 일정함을 확인할 수 있다. 바닥까지 내려가는데 걸리는 시간 $T_0$가 정해지면 원의 반지름 $gT_0^2/\pi$이 결정되어 곡선 모양이 자동으로 정해진다.
Cycloid는 이 성질 이외에도 일정한 중력하에서 두 지점을 연결하는 곡선을 움직일 때 최단 시간을 주는 곡선이기도 하다(brachistochrone curve)
등시진자
단순진자는 원호 위에서 반복운동을 한다. 수직에 대해 벌어진 각이 $\theta$일 때 각에 대한 운동 방정식은 $$ \ddot \theta = - \frac{g}{L} \sin \theta.$$ 진폭이 작은 경우 ($|\theta| \ll 1$) 윗 식은 용수철 진
kipl.tistory.com
'Mathematics' 카테고리의 다른 글
| Fourier Series를 이용한 Isoperimetric Inequality 증명 (1) | 2023.02.01 |
|---|---|
| Snell's law and Brachistochrone Curve (0) | 2023.01.25 |
| Fourier transform of the Heviside step function (0) | 2023.01.12 |
| Integration along a branch cut-015 (0) | 2022.12.17 |
| Gibbs Phenomenon (0) | 2022.05.06 |




