Geometry & Recognition

$$I = \int_0^1 \left( \frac{1-x}{x} \right)^{x/ \pi } \sin xdx =  \frac{1}{2}e^{-1/\pi} \approx  0.363689$$

다음의 복소함수 

$$  f(z) = \exp \left(   \frac{z}{\pi}\log \frac{z-1}{z}\right)$$

의 contour 적분을 고려하자.

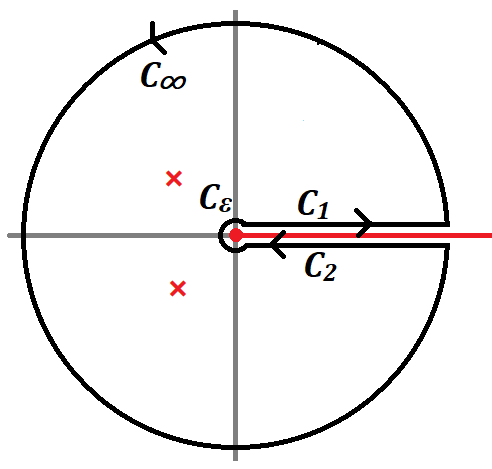
Branch point가 $z=0,1$이므로 cut line을 구간 $[0,1]$로 잡자. 그리고 위상은 $\sin(x)$을 나타나게 하기 위해서 $$ 0\le \text{arg}(z)\le 2\pi,  \quad -\pi \le \text{arg}(z-1) \le \pi$$

로 선택한 후 그림과 같은 개뼈 경로와 반지름 $R>1$인 원 $C_R$에 대해서 적분을 한다. $f(z)$는 무한대에서 residue을 가지는데 

$$ f(z=1/t) =  e^{ \frac{1}{\pi t} \log(1-t)}= e^{-1/\pi} - \frac{e^{-1/\pi}}{2\pi} t + \cdots \\ \to  \text{Res} f(z\to \infty) = \frac{e^{-1/\pi}}{2\pi}$$ 따라서 

$$ \int_{C_R} f(z) dz= -2\pi i  \times \text{Res}f(z\to \infty) = -i e^{-1/\pi} $$ $C_1$에서 $z= x e^{i0}$, $z-1 = (1-x)e^{i \pi}$이고, $C_2$에서 $z= x e^{i 2\pi}$, $z-1=(1-x) e^{-i \pi}$이므로\begin{align} \left( \int_{C_1} + \int_{C_2} \right) f(z)dz &= \int _0^1 \exp\left[ \frac{x}{\pi} \left( \log\left|\frac{1-x}{x}\right| + i \pi\right) \right]dx + \int_1^0 \exp\left[ \frac{x}{\pi}\left( \log \left| \frac{1-x}{x} \right|- i \pi  \right) \right]dx \\ &= 2i \int_0^1 \left( \frac{1-x}{x} \right) ^{x/\pi}  \sin x dx  = 2i I  \end{align}

그리고 개뼈 경로의 둥근부분에서 적분은 0으로 수렴하므로 residue 정리에 의해 

$$  \int_{C_1 +C_2 + C_\epsilon + C'_\epsilon} f(z)dz + \int_{C_R} f(z)dz = 0 \\ \to 2i I = 2\pi  i \times \text{Res}f(z\to \infty)\\ \to \qquad I = \frac{1}{2}e^{-1/\pi} $$

$$I= \int_0^\infty \frac{x^{a-1} dx }{ x^2 + x+1} =  \frac{2\pi}{\sqrt{3}} \csc(\pi a) \sin\frac{\pi (1-a)}{3},~~ 0<a < 2$$

함수 $f(z)$

$$ f(z) =   \frac{z^{a-1}}{z^2 + z+1}$$

의 conttour 적분을 고려하자. $z=\frac{-1+i\sqrt{3}}{2}=\gamma, ~\frac{-1-i\sqrt{3}}{2}=\gamma ^2$가 $f(z)$의 simple pole 위치다. 그리고 residue값은

\begin{align} \text{Res}f( \gamma) &= \frac{\gamma^{a-1}}{\gamma - \gamma^2}= \frac{i}{\sqrt{3}} e^{i\pi a} e^{-i \pi (a-1)/3} \\ \text{Res}f(\gamma^2)  &= \frac{\gamma^{2(a-1)}}{\gamma^2- \gamma} = \frac{-i}{\sqrt{3}}e^{i\pi a} e^{i\pi(a-1)/3}\end{align} $x^a$ 때문에 branch cut을 선택해야 하는데 $+x$으로 잡자. 그러면 $0   \le \text{arg}(z) \le 2\pi $로 잡을 수 있다.

경로 $C_1$에서 $z= x e^{i0}, ~(x:0\to \infty)$이므로 

$$ \int_{C_1} f(z)dz = \int_0^\infty \frac{x^{a-1}dx}{x^2+x+1}  = I$$

경로 $C_2$에서 $z= x e^{i 2\pi},~(x:\infty \to 0)$이므로

$$ \int_{C_2} f(z)dz = e^{i 2\pi (a-1)} \int_\infty^0 \frac{x^{a-1} dx}{x^2 + x+1} = - e^{i 2\pi a} I $$

그리고 $C_\epsilon$과 $C_\infty$에서는 적분은 0이다:$$\int_{C_\epsilon} f(z)dz \sim \epsilon^a  \to0\\ \int_{C_\infty} f(z)dz \sim \frac{1}{R^{2-a}}\to 0$$따라서

$$ \oint f(z)dz = 2\pi i [ \text{Res}f(\gamma) + \text{Res}f(\gamma^2)]$$

$$ \to \quad  I = \frac{2\pi}{\sqrt{3}} \csc(\pi a)\sin \frac{\pi (1-a)}{3}$$

$$I = \int_0^1 \frac{x^{\alpha} (1-x)^{1-\alpha}dx}{2-x} = \frac{\pi(1+\alpha -2^\alpha)}{\sin \pi \alpha } , ~~~|\alpha |  <1$$

복소평면에서 함수 $f(z)$

$$ f(z) = \frac{z^{\alpha} (1-z)^{1-\alpha}}{2-z}$$의 경로적분을 고려하자. 

$z=0,2$이 branch point이므로 그림과 같이 cut line과 개뼈 경로를 선택한다. 이 경우 가능한 위상 선택은 

$$ -\pi \le \arg (z) \le\pi, \quad   0 \le \arg(1-z) \le 2\pi$$

$z=2$는 $f(z)$의 simple pole이고 residue는 

$$ \text{Res}f(z=2) =- 2^{\alpha}(e^{i\pi} )^{1-\alpha} = 2^\alpha e^{-i\pi \alpha}$$

이다. 또 $ z\to\infty$일 때 전개를 하면 

$$ f(z) =\frac{(-1)^{1-\alpha} (1-1/z)^{1-\alpha} }{-(1-2/z)}= e^{-i \pi \alpha} \left( 1 + \frac{1+ \alpha}{z}+\cdots \right)$$

이므로 무한대에서 residue가 존재한다.

$$ \text{Res} f(z\to\infty)= - e^{-i\pi \alpha} (1+\alpha)$$

$C_\epsilon$, $C_\epsilon'$에서 경로적분이 $0$이므로 다음이 성립한다.

$$ \int_\text{dogbone} f(z) + \int_{C_R} f(z) = 2\pi i \times  \text{Res}f(z=2) \\ \to \int_\text{dogbone}=2\pi i \times \big[ \text{Res}f(z\to\infty) + \text{Res}f(z=2) \big]$$

그리고 $C_1$에서 $z= x e^{i0}$, $1-z=(1-x)e^{2i\pi}$이므로 

$$ \int_{C_1} f(z) dz =  \int_0^1 \frac{x^{\alpha}(1-x)^{1-\alpha}e^{i2\pi(1-\alpha)}dx}{2-x} = e^{-i2\pi \alpha} I $$

$C_2$에서는 $z= x^{i0}$, $1-z = (1-x) e^{i0 }$이므로

$$ \int_{C_2} f(z)dz =  e^{-i\pi(1-\alpha)}\int_1^0 \frac{x^{\alpha}(1-x)^{1-\alpha} dx}{2-x} = -I$$

따라서 residue 정리에 의해서

$$ (e ^{-i2\pi \alpha} - 1) I = 2\pi i \big[ 2^\alpha e^{-i \pi \alpha} - (1+\alpha) e^{-i\pi\alpha} \big]\\ \to ~~I = \frac{\pi}{ \sin \pi \alpha } (1+\alpha - 2^{\alpha})$$