Geometry & Recognition

$t=0$일 때 $x=0$인 경계에 온도 $u_0=1$인 열원에 접촉을 시킬 때 $t>0, x>0$에서 온도분포는 (열전도계수=1)는 (1차원) 열방정식에 의해서 결정된다.(1차원 확산방정식도 동일한 형태이다)

$$ \frac{\partial^2 u(x,t) }{\partial x^2} = \frac{ \partial u(x,t)} {\partial t}, ~~ u(x=0, t)=  \theta(t)$$

이 방정식을 Laplace변환을 이용해서 풀어보자. 양변에 Laplace 변환을 취하면 $\bar u(x,s) \equiv {\cal L} [u](x,s)$

$$ \frac{\partial ^2   \bar u(x,s)}{ \partial x^2 } = s \bar u(x,s) - u (x, 0) = s \bar u(x,s)$$ 

$\bar u(x, s=0) = 1 /s$이므로 위 방정식의 해는

$$ \bar u(x, s) = e^{  - x \sqrt{s}} \bar u(x, 0)= \frac{ e^{-x\sqrt{s}} }{s}$$

시간에 대한 해를 구하기 위해 역 Laplace변환을 취하면 

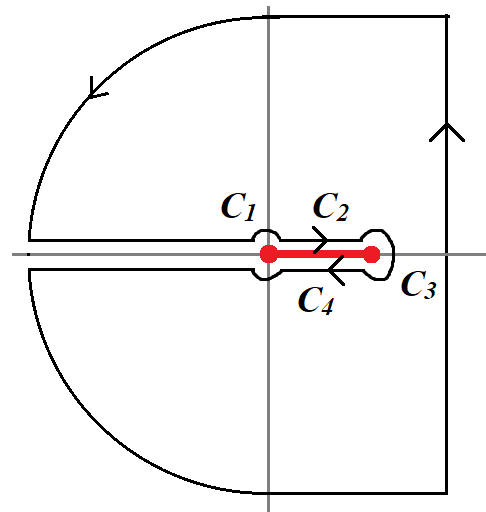
$$ u(x,t) =\frac{1}{2\pi i} \int_{\gamma-i\infty}^{\gamma + i\infty}  \frac{e^{- x\sqrt{s}} }{s}  e^{st} ds$$ $z=0$이 $\sqrt{z}$의 branch point이므로 이 적분을 구하기 위해서 $-x$축을 branch cut으로 하는 그림과 같은 경로에서 적분을 고려하자.

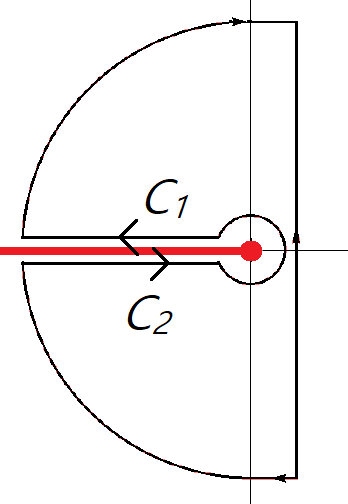
이 경로 내부에서 피적분함수가 analytic 하므로 $$ \oint e^{zt }e^{- x\sqrt{z}} \frac{dz}{z}=0$$이다. 따라서

$$ u(x, t) =\frac{1}{2\pi i}  \int_C e^{zt } e^{- x \sqrt{z}} \frac{dz}{z}$$

로 쓸 수 있다. 경로 $C_1, C_2$ 그리고 $z=0$을 감싸는 경로에서 적분만 기여한다. 우선 경로 $C_1$에서 $z= \rho  e^{i\pi}~(\rho:0\to \infty)$이므로 

$$ \int_{C_1}   =\int_0^\infty  e^{- \rho t } e^{-i x \sqrt{\rho} } \frac{d\rho}{\rho} $$

경로 $C_2$에서 $z=\rho e^{-i \pi}~~(\rho: \infty \to 0)$이므로 

$$ \int_{C_2} = \int_\infty^0 e^{-\rho t} e^{i x \sqrt{\rho} } \frac{d \rho}{\rho}$$

그리고 $z=0$ 둘레에서 $z=\epsilon e^{i \theta}$이므로

$$ \int_{C_\epsilon} = 2\pi i $$

이므로

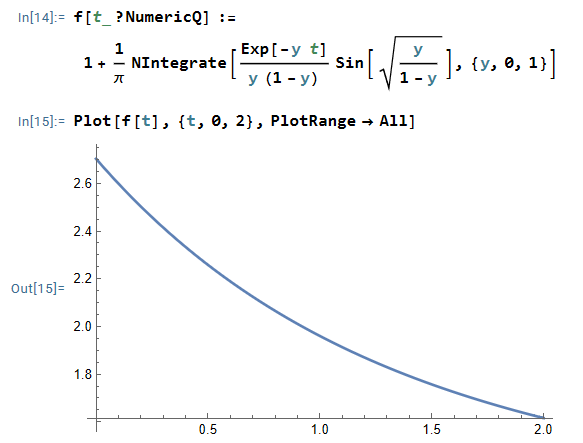
$$ u(x,t ) = 1 - \frac{1}{\pi} \int _0^\infty e^{-\rho t} \sin (x\sqrt{ \rho}) \frac{d \rho}{\rho}$$

 $\xi = \sqrt{\rho}$로 치환하면

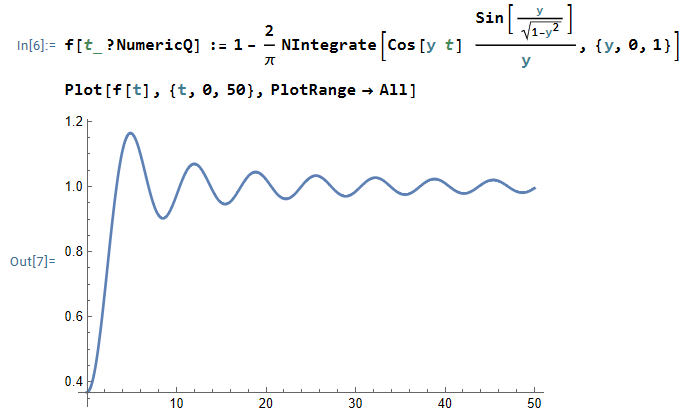
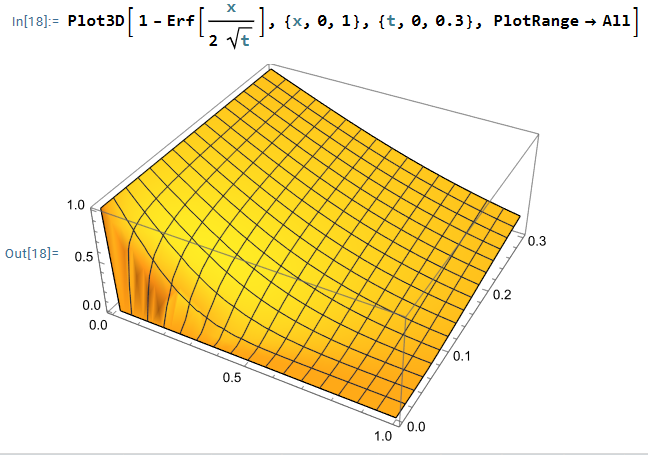
$$ u(x,t) = 1 -\frac{2}{\pi} \int_0^\infty e^{-\xi^2 t} \sin ( x\xi) \frac{d\xi}{\xi} \\=1- \text{Erf}\left( \frac{x}{2\sqrt{t}} \right)$$

처럼 error 함수로 표현할 수 있다.

$$ f(t)= {\cal L}^{-1} \left[ \frac{1}{s(s-1)} \exp\left(-\sqrt{\frac{s-1}{s}} \right)\right](t)$$

그림과 같은 경로에서 $\oint F(z) e^{zt} dz = 0$이므로

$$f(t) =\frac{1}{2\pi i} \int_{\gamma-i \infty}^{\gamma +i \infty} F(s) e^{st} ds = - \frac{1}{2\pi i} \int_{C} \frac{e^{zt}}{z(z-1)} \exp\left(-\sqrt{\frac{z-1}{z}} \right) dz$$

$$ -\pi \le  \arg(z), \arg(z-1) \le \pi$$

$C_1$에서 $z=\epsilon e^{i \theta}$이므로

$$\int_{C_1} =  0$$

$C_3$에서 $z= 1+ \epsilon e^{i \theta} ~(\theta: \pi \to -\pi)$,

$$\int_{C_3} \frac{ e^{zt}}{z(z-1)} \exp\left( -\sqrt{\frac{z-1}{z}}\right) dz = -2\pi i e^{t}   $$ 

$C_2$에서 $z=x e^{i  0}$, $z-1= (1-x) e^{i \pi}~(x:0\to 1)$이므로

$$ \int_{C_2} =  \int_0^1 \frac{e^{xt} }{x(x-1)} \exp\left( - i\sqrt{\frac{1-x}{x}} \right) dx$$

$C_4$에서 $z=x e^{i 0}$, $z-1=(1-x) e^{-i \pi}~(x:1\to0)$이므로

$$\int_{C_4} =\int_1^0 \frac{ e^{xt}} { x(x-1)} \exp\left( i\sqrt{\frac{1-x}{x}} \right) dx$$

따라서 정리하면

$$f(t) = e^{t} + \frac{1}{\pi} \int_0^1 \frac{e^{xt}}{x(x-1)} \sin \left( \sqrt{\frac{1-x}{x}} \right)  dx \\ = e^t\left[ 1+ \frac{1}{\pi} \int_0^1\frac{e^{-yt}}{y(1-y)}\sin \left( \sqrt{\frac{y}{1-y}} \right)dy \right]$$

$$f(t) = {\cal L}^{-1} \left[ \frac{1}{s}\exp\left( -\frac{s}{\sqrt{1+s^2}}\right) \right](t)$$

역 Laplace 변환을 Bromwich 적분으로 표현하면 $$f(t) = \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma +i\infty}  F(s) e^{st}ds=\frac{1}{2\pi i} \int_{C} \frac{1}{z}\exp \left(- \frac{z}{\sqrt{1+z^2}} +z t \right) dz$$ 적분경로 $C= \{C_1+C_2+C_3+C_4+C_\epsilon + \text{half circle}\}$는 그림의 폐경로에서 오른쪽  $z=\gamma$ 을 통과하는 수직선을 제외한 나머지 부분이다. 제곱근 함수 때문에 branch cut을 $z=\pm i$을 연결하는 선분으로 잡는다. 이 경우 위상은 $$ -\frac{\pi}{2} \le \arg(z-i) , ~\arg(z+i) \le \frac{3\pi}{2}$$ 로 잡을 수 있다. 

그러면 각 경로에서,

$$ C_1:~~z=y e^{i\pi/2}, ~ z-i=(1-y) e^{i 3\pi/2}, ~z+i= (1+y)e^{i\pi/2},~y:1\to0$$

$$ C_2:~~z=y e^{i\pi/2}, ~ z-i=(1+y) e^{ - i \pi/2},~z+i = (1-y)e^{i\pi/2},~y: 0\to1$$

$$ C_3:~~z=y e^{-i\pi/2}, ~ z-i=(1+y) e^{-i \pi/2},~z+i = (1-y)e^{i\pi/2},~y:0\to1$$

$$ C_4:~~z=y e^{-i\pi/2}, ~ z-i=(1-y) e^{i 3\pi/2},~z+i = (1+y)e^{i\pi/2},~y:1\to0$$

따라서 

$$ \int_{C_1} = \int_1^0 \exp\left(  \frac{iy}{\sqrt{1-y^2} } + iyt\right) \frac{dy}{y}$$

$$ \int_{C_2} = \int_0^1 \exp\left(  \frac{-iy}{\sqrt{1-y^2} } + iyt\right) \frac{dy}{y}$$

$$ \int_{C_3} = \int_1^0 \exp\left(  \frac{iy}{\sqrt{1-y^2} } - iyt\right) \frac{dy}{y}$$

$$ \int_{C_4} = \int_0^1 \exp\left(  \frac{-iy}{\sqrt{1-y^2} } - iyt\right) \frac{dy}{y}$$

그리고  simple pole $z=0$을 감싸는 적분은 ($z=\epsilon e^{i \theta}$)

$$ \int_{C_\epsilon} = 2\pi i  $$

이므로 $f(t)$는 다음과 같이 쓸 수 있다.

$$ f(t) = 1 -\frac{2}{\pi} \int_0^1 \cos (yt) \sin \left( \frac{y}{\sqrt{1-y^2}} \right) \frac{dy}{y}$$