Geometry & Recognition

$$ I = \int_1^\infty \frac{\arctan(x)dx}{x(x^2 + a^2) }  = \frac{\pi  \log(1+a)}{a^2}, ~~~~0<a<1$$

$$ f(z) = \frac{\arctan(z)}{z(z^2 + a^2)}= \frac{\frac{1}{2i}\log\frac{i-z}{i+z}}{z(z^2 + a^2)}$$을 그림과 같은 경로에서 적분하자.

그러면 $$ I+  \left( \int_{C_1+C_3} + \int_{C_2} + \int_{C_\infty} \right) f(z) dz = 2\pi i \times \text{Res}f(ia)$$

\begin{gather} \int_{C_1 +C_3} f(z) dz = - \frac{1}{2i} \int_{C_3} \frac{\log \left| \frac{i-z}{i+z}\right| + i ( \arg(i-z) + 2\pi  -\arg(i+z)) }{z(z^2 + a^2)}dz\\ + \frac{1}{2i} \int_{C_3} \frac{\log\left| \frac{i-z}{i+z}\right|+ i(\arg(i-z)-\arg(i+z))}{z(z^2 + a^2)}dz  \\ =  -\pi \int_{i}^{i \infty} \frac{dz}{z(z^2 + a^2)} = -\pi \int_1^\infty \frac{dy}{y( a^2 - y^2)} \\=-\frac{\pi}{2a^2} \int_{1}^\infty  \left( \frac{2}{y} -\frac{1}{a+y}+\frac{1}{a-y}\right)dy = -\frac{\pi}{2a^2} \log (1-a^2) \end{gather} 그리고 

$$\text{Res}f(ia) = \frac{i}{4a^2} \log \frac{1-a}{1+a}$$이고  $C_2, C_\infty$에서 적분이 0으로 수렴하므로 

$$  I =         \frac{\pi  \log(1+a)}{a^2 }$$

$$I =  \int_0^1 \frac{1}{1+x^2} \sqrt{\frac{x^3}{1-x}}dx  = \pi \left( 1 -\frac{\sqrt{\sqrt{2} +1}}{2} \right) \approx 0.223113\times \pi $$

복소함수 

$$ f(z) = \frac{1}{1+z^2} \sqrt{\frac{z^3}{1-z}}$$를 그림과 같은 경로에서 적분하자. Branch cut은 $z=0$과 $z=1$을  잇는 선분으로 선택하면 위상은 

$$ -\pi \le \arg(z) \le \pi, \quad 0\le \arg(1-z)\le 2\pi$$로 잡을 수 있다. 그러면

$$ \left(\sum_k \int_{C_k} + \int _{C_\infty} \right)  = 2\pi i \times \left(\text{Res}(f(i)) + \text{Res}f(i) \right)$$

$C_1$에서 \begin{gather} z= x e^{i 0}~~(x:0 \to 1) \\ z-1 = (1-x)e^{i \pi} \to 1-z = (1-x) e^{i 2\pi} \\ \int_{C_1} = \int_0^1 \frac{1}{1+x^2} \sqrt{ \frac{x^3}{1-x}}\frac{e^{i0}}{e^{i\pi}} dx = - I\end{gather}

$C_3$에서 \begin{gather} z= xe^{i0}~~(x:1\to 0) \\ z-1 = (1-x) e^{i \pi} \to 1-z = (1-x) e^{i 0} \\ \int_{C_3} = \int_1^{0} \frac{1}{1+x^2} \sqrt{ \frac{x^3}{1-x}} \frac{e^{i0}}{e^{i0}} dx = -I \end{gather}

그리고 $z=\infty$에서 residue를 가지는데, 

$$ f(z) = \frac{1}{i z} + \cdots \\ \int_{C_\infty}  = - 2\pi i \times \left( -\frac{1}{i} \right) = 2\pi  $$이고 $\int_{C_2}\to 0$, $\int_{C_4} \to 0$이다. 그리고 $z= i $에서 residue는 

\begin{gather} z= e^{i\pi/2} \to \sqrt{z^3} = e^{i 3\pi/4} \\ z-1= \sqrt{2}e^{i 3\pi/4} \to 1-z= \sqrt{2} e^{i 7\pi/4} \to \sqrt{1-z}= \sqrt{\sqrt{2}} e^{i 7\pi/8} \\ \text{Res}f(i) = \frac{1}{i \sqrt{2\sqrt{2}} } e^{-i \pi/8} \end{gather} 또 $z=-i$에서 residue는 

\begin{gather} z=e^{-i \pi/2}\to \sqrt{z^3} = e^{-i3\pi/4} \\z+1=\sqrt{2} e^{i 5\pi/4} \to 1-z= \sqrt{2} e^{i\pi/4}\to \sqrt{1-z} = \sqrt{\sqrt{2}} e^{i \pi/8} \\ \text{Res}f(-i) = \frac{1}{i \sqrt{\sqrt{2}}} e^{i \pi/8}  \end{gather}이므로

$$ \sum \text{Res} = \frac{1}{ i\sqrt{\sqrt{2}}  } \cos \frac{\pi}{8} = \frac{\sqrt{\sqrt{2}+1} } {i 2}$$ 따라서 $$ -2I + 2\pi = 2\pi i \times \frac{  \sqrt{\sqrt{2}+1} }{i2} \\ I = \pi \left( 1 -\frac{\sqrt{\sqrt{2} + 1}}{2} \right)$$

$$   \frac{1}{2\pi i} \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{e^{st} ds}{\sqrt{s^2 -1}} = I_0(t)\\   \frac{1}{2\pi i} \int_{\gamma-i\infty}^{\gamma + i \infty} \frac{e^{st}ds }{\sqrt{s^2 +1}} = J_0 (t)$$

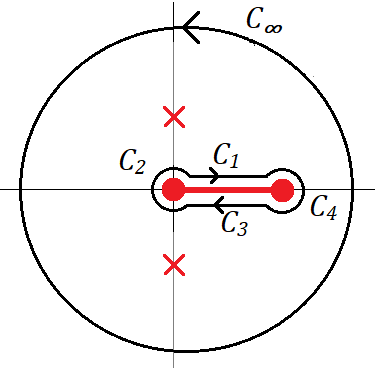
$$g(z)= \frac{e^{zt}}{\sqrt{z^2-1}}$$을 적분하기 위해서 그림과 같이 Browmwich contour를 선택하자. 위상은 $$ -\pi \le \arg(z-1), ~\arg(z+1) \le \pi $$

$\oint g(z) dz  = 0$이므로 

$$ I= \frac{1}{2\pi i} \int_{\gamma - i\infty}^{\gamma + i \infty} \frac{e^{st}ds}{\sqrt{s^2 - 1}} = - \sum_k  \frac{1} {2\pi i} \int_{C_k}   \frac{e^{zt}dz}{\sqrt{z^2-1}}$$ 

$C_2$에서 $z-1 = (1-x) e^{i \pi}$, $z+1 = (1+x) e^{i0}$이므로 

$$ \int_{C_2} =  \int_{-1}^1 \frac{e^{xt} dx}{ \sqrt{1-x^2} e^{i \pi/2} }= -i \int_{-1}^1 \frac{ e^{xt}dx}{\sqrt{1-x^2}}  $$

$C_4$에서 $z-1= (1-x) e^{-i \pi}$, $z+1=(1+x) e^{i 0}$이므로

$$ \int_{C_4} = \int _{1}^{-1} \frac{e^{xt}dx}{ \sqrt{1-x^2}e^{-i\pi/2}} = -i \int_{-1}^1 \frac{ e^{xt}dx}{\sqrt{1-x^2}} $$

이고 $\int_{C_1} = \int_{C_3}= 0$이므로  

$$ I = \frac{1}{\pi} \int_{-1}^{1} \frac{e^{xt} dx} {\sqrt{1-x^2}}$$

$ x= \cos \theta$로 치환하면

$$I= \int_{0}^\pi  e^{t  \cos \theta} d \theta  = \frac{1}{\pi}\sum_{k=0}^\infty  \int_{0}^{\pi } \frac{ (t \cos \theta)^k d \theta }{ k!} \\ = \frac{1}{\pi} \left[ \pi + \pi \frac{1}{2} \frac{t^2}{2!}+ \pi \frac{3}{4} \frac{1}{2} \frac{t^4}{4!} + \pi\frac{5}{6}\frac{3}{4}\frac{1}{2} \frac{t^6}{6!}+\cdots \right]  \\ = 1+ \frac{t^2}{2^2}+ \frac{t^4}{2^2 4^2 }+ \frac{t^6}{2^2 4^2 6^2}+\cdots =  \sum_{k=0}^ \infty \frac{(\frac{t}{2})^{2k}}{(k!)^2} \\= I_0(t)$$

$I_0(t)$는 modified Bessel function of the first kind and zero order.

Note: $$ {\cal L }^{-1} \left[\frac{1}{\sqrt{s^2 + 1}}\right] = J_0(t)$$

$$ -\frac{\pi}{2} \le \arg(z+i), ~\arg(z-i) \le \frac{3\pi}{2}$$

residue 정리에 의해서 

$$ I = \frac{1}{2\pi i}\int_{\gamma - i \infty} ^{\gamma + i \infty }\frac{ e^{st}ds}{\sqrt{s^2 + 1}} = -\sum_k \frac{1}{2\pi i} \int_{C_k} \frac{e^{zt} dz}{ \sqrt{z^2+1}}$$

$C_2$에서 $z- i = (1-y) e^{-i\pi/2}$, $z+i = (1+y) e^{\pi/2}$이므로

$$ \int_{C_2} = \int_{1}^{-1} \frac{ e^{i yt} (idy)}{ \sqrt{1- y^2}} = -i \int_{-1}^1\frac{ e^{-iyt}d y}{\sqrt{1-y^2}}$$ 

$C_4$에서 $z-i=(1-y) e^{i 3\pi/2}$, $z+i= (1+y) e^{i\pi/2}$이므로 

$$ \int_{C_4} = \int_{-1}^{1} \frac{e^{i yt}(i dy)}{\sqrt{1-y^2} e^{i\pi}} =- i\int_{-1}^{1} \frac{e^{iyt} dy }{\sqrt{1-y^2}} $$

따라서 $$\int_{C_2 +C_4} = -2i \int_{-1}^2 \frac{\cos(yt)dy}{\sqrt{1-y^2}}$$ 

$$ I = \frac{1}{\pi} \int_{-1}^{1} \frac{ \cos(yt) dy}{\sqrt{1 -y^2}}= \frac{1}{\pi} \int_{-\pi}^{\pi} \cos( t \sin \theta) d \theta = J_0(t)$$

$J_0(t)$는 Bessel function of the first kind  and zero order.