$$ I = \int_0^\infty \frac{\log(1+x^2) }{x^2}=\pi$$

복소함수
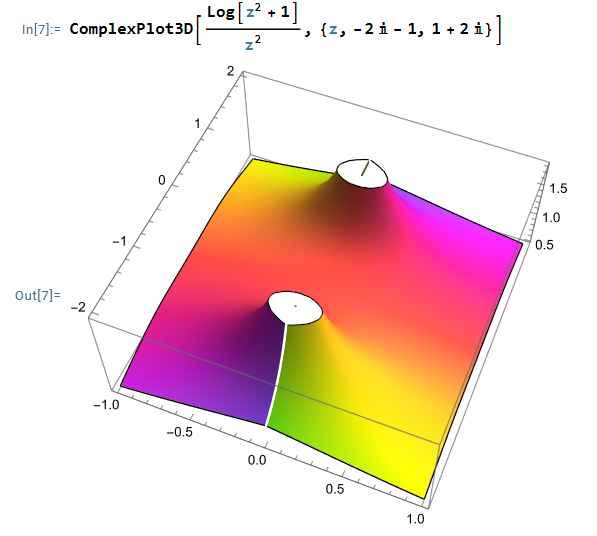
$$ f(z) = \frac{ \log( 1+ z^2) }{ z^2 }$$
을 contour 적분을 이용해서 구하자. $f(z$)의 branch point가 $z=i,-i, \infty$이므로, branch cut은 그림처럼 잡자. 그러면 위상은
$$ -\frac{3\pi}{2} \le \text{arg}(z-i) \le \frac{\pi}{2},~~ -\frac{\pi}{2}\le \text{arg}(z+i) \le \frac{3\pi}{2}$$로 잡을 수 있다. 그림과 같이 cut-line을 도는 contour에 대한 $f(z)$의 적분을 고려하면
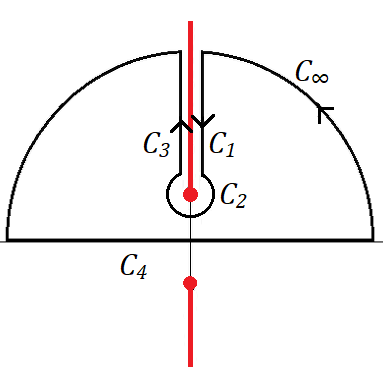
$C_1$에서 $$z= x e^{i\pi/2}~(x: \infty \to 1) \\ z+i = (x+1) e^{i\pi/2},~~~z-i=(x-1) e^{i\pi/2} \\ \log(z^2+1) = \log|z^2-1| + \text{arg}(z-i) + \text{arg}(z+i) = \log(x^2-1) + i\pi$$이므로
$$\int_{C_1} f(z)dz = \int_\infty^1 \frac{\log(x^2-1)+i\pi}{-x^2}(e^{i\pi/2} dx)=i \int_1^\infty \frac{\log(x^2-1)+i\pi }{x^2}dx$$
$C_3$에서 $$z=x e^{-i\pi} ~(x: \to \infty)\\ z+i = (x+1) e^{i\pi/2}, ~~~z-i= (x-1) e^{-i 3\pi/2} \\ \log(z^2+1)=\log |z^2+1| + \text{arg}(z-i)+\text{arg}(z+i) = \log(x^2-1) -i\pi$$이므로
$$ \int_{C_3} f(z)dz = \int_1^\infty \frac{\log(x^2-1) -i \pi}{-x^2 }(e^{i\pi/2} dx)=-i \int_1^\infty \frac{\log(x^2-1)- i \pi }{x^2 } dx$$
$C_4$에서
$$ \int_{C_4} f(z) dz = \int_{-\infty} ^\infty \frac{ \log(1+x^2)}{x^2} dx = 2I $$
그리고 $C_2$에서 $z=\epsilon e^{i \theta}$이므로
$$\int_{C_2} f(z) dz = O( (\log \epsilon) \epsilon) \rightarrow 0,$$
$C_\infty$에서 $z= R e^{i \theta}$이므로
$$\int_{C_\infty} f(z) dz = O((\log R)/R) \rightarrow 0.$$
Contour 내부에서 analytic 하므로
$$\oint f(z) dz = 0 ~\to ~2I= 2\pi \int_1^\infty \frac{dx}{x^2} = 2\pi ~~~\to ~~ I =\pi$$
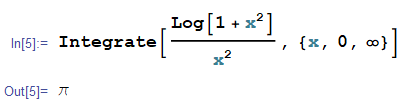
'Mathematics' 카테고리의 다른 글
| 주어진 길이의 폐곡선으로 가둘 수 있는 최대 면적의 도형은? (1) | 2020.02.15 |
|---|---|
| Integration along a branch cut-005 (0) | 2017.07.02 |
| Integration along a branch cut-004 (0) | 2017.06.29 |
| Integration along a branch cut-002 (2) | 2017.06.28 |
| Integration along a branch cut-001 (0) | 2017.06.27 |



