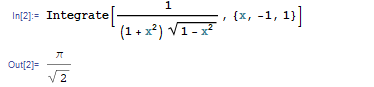Geometry & Recognition

$$I = \int_0^1 \frac{dx}{\sqrt{x(1-x)}} = \pi$$

복소함수

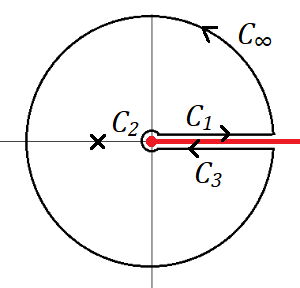
$$f(z) = \frac{1}{\sqrt{z(1-z)}}$$을 그림과 같은 contour에 대해서 적분을 한다.

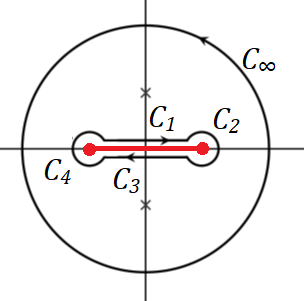
$f(z)$는 $z=0, 1$이 branch point이므로 그림처럼 branch cut을 선택한다: 위상은 $ -\pi \le \arg(z) \le \pi$, $0 \le \arg(1-z) \le  2\pi$. 그러면 $$ \left(\int_{C_1}+\int_{C_2}+ \int_{C_3}+ \int_{C_4} \right) f(z)dz = \int_{C_\infty} f(z)dz$$

$C_\infty$를 $z=R e^{i\theta}, ~\theta=0\to 2\pi$로 매개화하면 $$\int_{C_\infty} f(z) dz = \lim_{R\to\infty} \int_0^{2\pi} \frac{ iR e^{i \theta} d \theta }{iR e^{i\theta}}= 2\pi $$

경로 $C_1$에 대해서는 $z=x e^{i0}$, $z-1=(1-x)e^{i\pi}\to1-z=(1-x)e^{i2\pi}~(x:1\to0)$ 이므로 ($1-z= \text{Rot}_{\pi} (z-1)$)

$$\int_{C_1} f(z)dz = \int_1^0 \frac{dx}{\sqrt{x(1-x)} e^{i \pi }} = \int_0^1 \frac{dx}{\sqrt{x(1-x)}}=I$$

$C_3$에서 $z=x^{i 0 }$, $z-1=(1-x) e^{i\pi} \to 1-z=(1-x) e^{i 0}~(x:0\to1)$이므로

$$ \int_{C_3} f(z) dz = \int_0^1 \frac{dx}{\sqrt{x(1-x)}} = I$$

그리고, $C_2:~1-z=\epsilon e^{i\theta}$, $C_4: ~z=\epsilon e^{i\theta}$에서

$$\int _{C_{2,4}}f(z) = O(\sqrt{\epsilon}) \rightarrow 0$$이므로

$$\int_{C_1+C_2 + C_3 +C_4} f(z)dz = \int_{C_\infty} f(z) dz ~\to~ I=\pi$$

$$ I = \int_0^\infty \frac{\log(1+x^2) }{x^2}=\pi$$

복소함수

$$ f(z) = \frac{ \log( 1+ z^2) }{ z^2 }$$

을 contour 적분을 이용해서 구하자. $f(z$)의 branch point가 $z=i,-i, \infty$이므로, branch cut은 그림처럼 잡자. 그러면 위상은

$$ -\frac{3\pi}{2} \le \text{arg}(z-i) \le \frac{\pi}{2},~~ -\frac{\pi}{2}\le \text{arg}(z+i) \le \frac{3\pi}{2}$$로 잡을 수 있다. 그림과 같이 cut-line을 도는 contour에 대한 $f(z)$의 적분을 고려하면

$C_1$에서 $$z= x e^{i\pi/2}~(x: \infty \to 1) \\ z+i = (x+1) e^{i\pi/2},~~~z-i=(x-1) e^{i\pi/2} \\ \log(z^2+1) = \log|z^2-1| + \text{arg}(z-i) + \text{arg}(z+i) = \log(x^2-1) + i\pi$$이므로 

$$\int_{C_1} f(z)dz = \int_\infty^1 \frac{\log(x^2-1)+i\pi}{-x^2}(e^{i\pi/2} dx)=i \int_1^\infty \frac{\log(x^2-1)+i\pi }{x^2}dx$$

$C_3$에서 $$z=x e^{-i\pi} ~(x: \to \infty)\\ z+i = (x+1) e^{i\pi/2}, ~~~z-i= (x-1) e^{-i 3\pi/2} \\ \log(z^2+1)=\log |z^2+1| + \text{arg}(z-i)+\text{arg}(z+i) = \log(x^2-1) -i\pi$$이므로

$$ \int_{C_3} f(z)dz = \int_1^\infty \frac{\log(x^2-1) -i \pi}{-x^2 }(e^{i\pi/2} dx)=-i \int_1^\infty \frac{\log(x^2-1)- i \pi }{x^2 } dx$$ 

$C_4$에서  

$$ \int_{C_4} f(z) dz = \int_{-\infty} ^\infty \frac{ \log(1+x^2)}{x^2} dx = 2I $$

그리고 $C_2$에서 $z=\epsilon e^{i \theta}$이므로

$$\int_{C_2} f(z) dz = O( (\log \epsilon)  \epsilon) \rightarrow 0,$$

$C_\infty$에서 $z= R e^{i \theta}$이므로

$$\int_{C_\infty} f(z) dz = O((\log R)/R) \rightarrow 0.$$

Contour 내부에서 analytic 하므로

$$\oint f(z) dz = 0 ~\to ~2I= 2\pi \int_1^\infty \frac{dx}{x^2} = 2\pi ~~~\to ~~ I =\pi$$

$$I = \int_0^\infty \frac{x^adx}{(1+x)^2  } = \frac{\pi a}{\sin \pi a } ~~~~(-1 < a<1) $$

복소함수

$$ f(z) = \frac{z^a}{(1+z)^2}$$

을 그림의 contour를 따라 적분한다. $f(z)$는 $z=0,\infty$이 branch point 이므로 cut line을 $+x$ 축으로$(0\le\arg(z)\le2\pi$) 잡았다. $z=-1$은 double pole이다.

경로 $C_1$에서 $ z= x e^{i 0} ~~(x: 0 \to \infty)$이므로

$$\int_{C_1} f(z)dz = \int_0^\infty \frac{x^a }{(1+x)^2 }dx = I$$

경로 $C_3$에서 $ z= x e ^{i 2\pi} ~~(x: \infty \to 0)$이므로

$$ \int_{C_3} f(z) dz = \int_\infty^0 \frac{x^a e^{i 2\pi a} }{(1+x)^2  }dx = - e^{i 2\pi a }I $$

경로 $C_2$에서 $z=\epsilon e^{i \theta}~(\theta:0\to 2\pi)$이므로

$$\int_{C_2}  f(z)dz = O( \epsilon^{1+a} ) \rightarrow 0.$$

경로 $C_\infty$에서 $z= R e^{ i \theta}$로 쓰면

$$\int_{C_\infty} f(z) dz = O(R^{a-1}) \rightarrow 0.$$

그리고, $z=-1=e^{i\pi}$에서 residue값은

$$\text{Res}f(z=e^{i\pi} ) =\frac{dz^a}{dz} (z=e^{i\pi}) = a(e^{i\pi})^{a-1}=-a e^{i\pi a}$$ 따라서 residue 정리에 의해

$$\sum \int_{C_k} f(z) dz = 2\pi i \times \text{Res}f(e^{i \pi})  $$

$$ (1- e^{i2\pi a} ) I = 2\pi i (-a e^{i\pi a}) ~~~~\to ~I= \frac{\pi a}{\sin \pi a}$$

$$I= \int_{-1}^{1} \frac{dx}{ (1+x^2)\sqrt{1-x^2 }}=\frac{\pi}{\sqrt{2}} $$

복소평면에서 함수 $$f(z) =  \frac{1}{(1+z^2 ) \sqrt{ 1-z ^2 }} $$

의 contour integral을 이용해서 적분을 구하자. $f(z)$는 $z= \pm 1$을 branch point로 가지므로 branch cut은 이 두 branch point을 연결하는 선으로 잡는다. 위상은 각각 $-\pi \le \arg(1+z) \le \pi$, $0\le \arg(1-z) \le 2\pi$로 선택한다. $z=\pm i$ 는 simple pole이다.

Branch cut 둘레를 도는 경로와 무한대를 도는 경로를 따라 적분하면 simple pole $z=\pm i$을 포함하므로 Cauchy의 residue 정리에 의해서

$$\left( \int_{C_1+C_2+C_3+C_4} + \int_{C_\infty} \right) f(z)dz = 2\pi i \times \text{Res} (z= \pm i)$$$C_1$에서 $$z+1 = (1+x) e^{i0}~(x:-1\to1) \\z-1=(1-x) e^{i\pi} ~\overset{\text{Rot}(\pi)}{\longrightarrow} ~1-z = (1-x) e^{i2\pi}$$ $$ \int_{C_1} f(z) dz = \int_{-1}^1 \frac{dx}{ (1+x^2) \sqrt{1-x^2} e^{i\pi}}=-I$$

 $C_3$에서 $$z+1= (1+x) e^{i 0 }~(x:1\to -1) \\z-1= (1-x)e^{i\pi} ~\overset{\text{Rot}(\pi)}{\longrightarrow } ~1-z= (1-x) e^{i 0}$$ $$ \int_{C_3} f(z)dz = \int_1^{-1} \frac{dx}{(1+x^2) \sqrt{1-x^2} } = -I$$

$C_2$, $C_4$에서 $z\pm 1 = \epsilon e^{i \theta}$로 놓으면

$$\int _{C_2 , C_4}f(z) dz = O(\sqrt{\epsilon})\rightarrow 0,$$

$C_\infty$에서도 $z=R e^{i \theta}$로 표현하면,

$$\int_{C_\infty} f(z)dz = O({ 1/R^2 })\rightarrow 0.$$

$z=i$에서 residue은 $$  z+1 =\sqrt{2}e^{i\pi/4}, \\z-1= \sqrt{2} e^{i 3\pi /4} \to 1-z = \sqrt{2} e^{i7\pi/4}\\ \to \sqrt{1-z^2} = \sqrt{2} e^{i\pi} = - \sqrt{2}\\ \text{Res}f(z=i) =\frac{1}{(2i) (-\sqrt{2})} = \frac{i}{2 \sqrt{2}}$$ $z=-i$에서 residue는 $$z+1=\sqrt{2} e^{-i \pi/4} \\ z-1= \sqrt{2} e^{i 5\pi/4}\to 1-z=\sqrt{2} e^{ i\pi/4} \\ \to \sqrt{1-z^2} = \sqrt{2} \\ \text{Res} f(z=-i) = \frac{1}{(-2i) \sqrt{2}} = \frac{i}{2\sqrt{2}}$$

이므로 적분값을 얻을 수 있다.