Geometry & Recognition

공기 저항이 없을 때 물체를 $v_0$ 속력으로 위로 던지면 최고점에 올라가는데 걸리는 시간과 다시 내려오는데 걸리는 시간은 동일하게 $t_{ff} = v_0/g$로 주어진다. 공기 저항이 있는 경우는 어떻게 될지 구체적으로 계산해보자.

반지름이 $R$인 공 모양의 물체가 속력의 제곱에 비례하는 공기 저항(끌림힘) $D= \frac{1}{2} C\rho_{air} A v^2 \approx  0.2 \rho_{air} \pi R^2 v^2$을 받을 때, 올라가는 동안 운동 방정식은 (물체가 받는 공기의 부력도 고려해야 하지만 여기서는 무시한다. 부력은 $g$을 약간 줄이는 효과를 만든다)

$$  m \frac{dv}{dt} = -mg -\ 0.2   \rho_{air} \pi R^2  v^2, $$

$$ \rightarrow  \quad \frac{dv}{dt} = -g (1 + \gamma^2 v^2) , \quad\quad  \gamma^2 =  0.2 \frac{\pi R^2 \rho_{air} }{mg} .$$

$\gamma$는 내려오는 과정에서 terminal speed의 역수를 의미한다. 시간에 대해 적분을 해서 속도를 구하면,

$$ v(t) = \frac{1}{\gamma} \tan \Big( -\gamma gt + \arctan(\gamma v_0) \Big)$$

최고점에 도달하는데 걸리는 시간은 $v(t_{up})=0$ 에서

$$ t_{up} = \frac{1}{\gamma g} \arctan(\gamma v_0) = \frac{v_0}{g} \Big(1 - \frac{(\gamma v_0)^2}{3}+....\Big) $$

로 주어지므로 공기저항이 없을 때보다 더 짧다. 최고점의 높이는

$$ h_{max} = \int_0^{t_{up}} v(t) dt = \frac{1}{\gamma^2 g} \ln \sqrt{ 1 + (\gamma v_0)^2 } =\frac{v_0^2}{2g} \Big( 1- \frac{(\gamma v_0)^2}{2 }+...\Big)$$

로 주어지므로 역시 공기 저항이 없을 때보다 낮다.

다시 내려오는 과정에서 중력과 끌림힘이 반대방향이므로 운동 방정식은

$$ \frac{dv}{dt}= -g (1 -\gamma^2 v^2)$$

로 주어지고, 이를 적분하면 (출발 시간을 $t=0$으로)

$$ v(t) = -\frac{1}{\gamma} \tanh (\gamma g t)$$

이를 다시 적분하면 낙하시간에 따른 높이를 얻을 수 있다: $h(0)=h_{max}$

$$ h(t) = \frac{1}{\gamma^2 g} \ln \frac{ \sqrt{ 1+ (\gamma v_0)^2 } }{ \cosh( \gamma gt)}$$

따라서 바닥에 떨어지는데 걸리는 시간 $t_{dn}$은: $ h(t_{dn}) = 0$

$$t_{dn} = \frac{1}{\gamma g}\text{arccosh}\sqrt{1+(\gamma v_0)^2} =\frac{1}{\gamma g} \ln \left(\gamma v_0 + \sqrt{1+ (\gamma v_0)^2 } \right) = \frac{v_0}{g}\Big( 1  -  \frac{ (\gamma v_0)^2 }{6}+...\Big)$$

두 시간을 비교해보면 위로 던져진 물체가 최고점에 올라가는데 걸리는 시간보다 다시 내려오는데 걸리는 시간이 더 길다는 것을 볼 수 있다:

$$ {t_{dn} - t_{up}} \approx  \frac{(\gamma v_0)^2}{6} t_{ff}$$

$v_0 =10\text{m/s}$로 ($\rightarrow t_{ff} = 1.02\text{s}$, $v_{terminal} \approx 36.6\text{m/s}$) 야구공을 공중으로 던지는 경우를 예로 들면, 차이는 대략 0.013초 정도로 계산된다. 던지는 속력이 종단속력에 가깝거나 더 크면 근사식을 사용할 수 없고 정확한 계산식을 이용해야 한다.

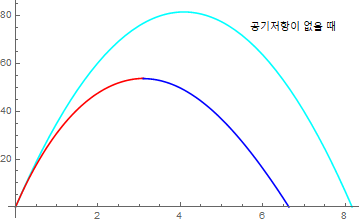
$v_0 = 40\text{m/s}$, $1/\gamma=36.6 \text{m/s}$ 일 때,

마찰 없이 바닥에서 움직일 수 있는 경사면$(M)$에 올려진 물체$(m)$가 정지상태에서 운동을 시작한다. 바닥에 내려왔을 때의  속력을 구하기 위해서 다음 과정을 따라 계산을 한다.

1. 다 내려온 후 바닥에서 물체와 경사면은 서로 반대 방향으로 움직인다(물체: $v_b$, 경사면:$V$)

2. 운동량 보존을 고려하면,

$$ m v_b = MV$$

3. 역학적 에너지가 보존되므로

$$\frac {1}{2} m v_b^2 + \frac {1}{2} MV^2 = mgh$$

두 식을 이용하면 경사면이 움직이는 속력은

$$V = \sqrt{  \frac {2gh}{(1+\frac {M}{m})\frac {M}{m}} }$$

로 주어진다.

그런데 kipl.tistory.com/118 에서 얻은 결과를 이용하면 (좀 복잡하지만: $\theta \rightarrow \alpha$)

$$V =\sqrt{ \frac {2gh}{(1+\frac {M}{m})( \frac {M}{m}  + \sin^2 \alpha) } }\cos\alpha$$

로 주어진다.

두 결과를 비교하면 다르다. 어디서 잘못이 들어온 것일까? 결과만 놓고 보았을 때 어느 계산이 맞는지 직관적으로 설명할 수 있는가?

막대의 끝과 쇠공은 같은 높이에서 떨어진다. 바닥에 먼저 닿는 물체는?

1. 막대

2. 쇠공

3. 동시에

데모 동영상을 볼 수 있는 곳:
• groups.spa.umn.edu/demo/mechanics/movies/1Q2050.mp4
• youtu.be/BV7TPvk__kE