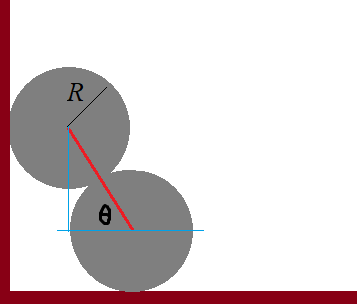
줄에 매달린 링의 꼭대기에 동일한 구슬 두 개가 있다. 충분히 무거운 구슬이 아래로 미끄러지는 운동을 시작하면 어느 순간에 링이 위로 솟구칠 수 있다. 그 조건은?

풀이:
구슬이 운동을 시작하면 원운동을 하는데, 처음에는 수직항력과 중력의 중심성분이 구심력 역할을 한다. 수직항력은 처음에는 링 중심에서 나가는 방향으로 작용하지만 $\cos \theta = 2/3$인 지점에 그 값이 0이 되고(구슬이 링에 꿰어져 있지 않다면 링에서 떨어진다), 그 이후에는 구슬을 계속 원운동 하게 만들기 위해서는 링 중심방향으로 작용해야 한다.
$$\text{circular motion:} ~~N + mg \cos \theta = \frac{mv^2}{R}~~~~~ \textstyle{\left(0< \cos \theta < \frac{2}{3}\right)}$$
이고 이때 구슬의 속력은 역학적 에너지 보존에 의해서
$$ v^2 = 2 Rg (1-\cos \theta)$$이므로
$$ N = mg ( 2 - 3\cos \theta)$$
이 수직항력의 반작용이 링에 작용하는데 수평성분은 양쪽 구슬에서 상쇄되므로 수직방향이 성분이 남는다. 이 수직방향 성분이 링의 무게보다 커지면 링은 위로 솟구칠 수 있다.
$$ R_y = 2N \cos \theta = 2mg(2 \cos \theta - 3\cos^2 \theta) \ge \frac{2}{3}mg$$
링에 작용하는 힘이 장력, 중력 그리고 $R_y$인데, $\text{min}(R_y)>Mg$이면 장력이 없더라도 링은 위로 가속할 수 있다.
$$ m > \frac{3}{2}M$$
'Physics > 역학' 카테고리의 다른 글
| 빙판 위에서 회전하는 동전 붙잡기 (0) | 2025.01.06 |
|---|---|
| 손에 충격을 덜 받으면서 나무 부러뜨리기 (0) | 2025.01.05 |
| 실린더의 최대속력은? (0) | 2025.01.03 |
| 미끄러지지 않을 조건은? (0) | 2025.01.03 |
| 체인이 움직이는 속력은? (1) | 2025.01.02 |