Bezier 곡선은 control points $\{ \mathbf {P}_i\}$의 선형 결합으로 주어진다:
$$\mathbf {B}(t) = \sum_{i=0}^{n} B_{ i, n} (t) \mathbf {P}_i , \quad B_{i,n}(t)=\left(\begin {array}{c} n \\ i \end {array} \right) t^i (1-t)^{n-i}.$$
Bernstein 다항식 $B_{i, n}(t)$이 control points 선형 결합의 가중치를 역할을 하는데 0과 1 사이의 양의 실수 값을 가진다. 그리고 이들 가중치의 합은 1이다:
$$ 0\le B_{ i, n}(t) \le 1, \quad i=0,1,2,... n , \quad 0\le t\le 1 $$
$$\sum_{i=0}^{n} B_{i, n}(t) = 1$$

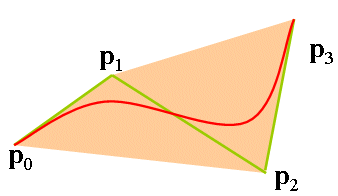
이는 Bezier 곡선이 control points가 만드는 convex region 내부에 있음을 의미한다. Bezier 곡선의 convexity 성질은 여러 좋은 특성을 준다. 몇 가지만 나열하면, 첫째가 Bezier 곡선은 항상 컨트롤 포인트의 convex hull 내에 놓이게 되므로 곡선의 제어 가능성을 보장한다. 둘째는 교차 여부를 쉽게 확인할 수 있다. 또한 culling을 가능하게 한다.
728x90
'Computational Geometry' 카테고리의 다른 글
| Bezier Smoothing (0) | 2021.04.23 |
|---|---|
| Flatness of Cubic Bezier Curve (0) | 2021.04.23 |
| De Casteljau's Algorithm (0) | 2021.04.22 |
| Arc Length of Bezier Curves (0) | 2021.04.21 |
| Bezier Curve Approximation of an Ellipse (0) | 2021.04.11 |




