Geometry & Recognition

Fermat의 원리는 빛이 한 지점에서 다른 지점으로 진행할 때 가장 시간이 적게 드는 경로를 따라 움직인다고 이야기하고 있다. 광속은 굴절률이 큰 곳에서 작아지므로 굴절률이 다른 두 지점을 통과하는 빛의 경로는 되도록이면 광속이 큰 곳을 오래 머무르는 경로를 선택하는 것이 시간상 유리하다. 따라서 매질의 경계면에서 진행방향이 꺾여야 된다. 구체적으로 광속이 $v_1$인 매질에서 $v_2$인 매질로 빛이 진행할 때 입사각  $\alpha_1$,  굴절각 $\alpha_2$인 경우  

$$ \frac{ \sin \alpha_1 }{v_1}= \frac{\sin \alpha_2}{v_2} \quad \Longrightarrow \quad \frac{v} {\sin \alpha} =\text{const}$$을 만족한다. 여기서 $\alpha$는 빛의 진행 방향을 매질 경계면에 수직인 방향에 대해 잰 각이다.

Fermat의 원리는 중력장에서 움직이는 물체에 대해서도 적용할 수 있다. 물체가 움직이면 중력 때문에 속력이 변하게 되므로 두 지점을 잇는 직선을 따라 움직이는 경로는 최단시간 경로가 되지 못한다. 구체적으로 한 지점에서 출발해서 처음보다 아래방향으로 $y$만큼  속력은 역학적 에너지 보존에 의해서 

$$  v^2 = 2gy$$

로 주어진다. 속력이 $y$값이 (아래로) 증가하면 빨라지므로 굴절률이 $\sqrt{y}\sim \sqrt{-U_\text{grav}}$에 반비례해서 연속적으로 감소하는 경우로 생각할 수 있다. 

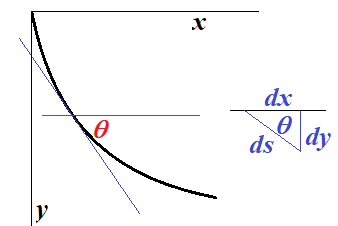
물체가 움직이는 경로상의 한 지점에서 접선이 수평에 대해 $\theta$만큼 기울어진 경우 입사각은 $\frac{\pi}{2}-\theta$이고, $\cos \theta = dx/ds$이다. 따라서 스넬의 법칙은 (제곱을 해서)

$$ \frac{v^2 }{ \sin ^2(\frac{\pi}{2}- \theta)} = \frac{v^2 }{\cos^2 \theta} = \frac{ 2gy}{(dx/ds)^2 } = \text{const} = 4gr$$

로 쓸 수 있다. $4gr$은 상수이다. 곡선의 미소길이

$$ ds =\sqrt{dx^2  + dy^2 } = \sqrt{1+(dy/dx)^2}dx$$

를 대입하면 중력장에서 물체가 움직이는 최소시간 경로는 다음의 비선형 미분방정식을 풀어서 얻을 수 있다.

$$ \Big( \frac{dy}{dx} \Big)^2 = \frac{2r}{y}-1\quad \Longrightarrow \quad dx = \sqrt{ \frac{y}{2r-y}}dy$$

잘 알려지다시피 이 방정식의 해는 cycloid 곡선으로 다음과 같이 표현할 수 있다. 

$$ x= r(\psi - \sin \psi ), \quad y = r (1- \cos \psi)$$

여기서 $\psi = {\pi-2\theta}$로 주어진다.

변분을 이용해서 구하는 경우는 https://kipl.tistory.com/186

$(1,1)$에서 $(0,0)$까지를 연결하는 일차 곡선 ($y=x$), 이차 곡선 ($y=x^2$), 6차 곡선 ($y=x^6$), 사분원 ($y=1-\sqrt{1-x^2}$) 그리고 cycloid ($x=1-R(\theta-\sin\theta), y=1-R(1-\cos\theta)$) 위를 움직이는 물체의 운동을 mathematica를 사용해서 animation으로 표현하는 방법을 알아보자. 중력가속도는 $g=1$로 놓는다. 적절한 generalized coordinate를 선택해서 Euler-Lagrange equation을 이용하면 운동방정식을 쉽게 구할 수 있다.

(A)  곡선이 $y=f(x)$의 형태로 주어지는 경우 운동방정식은

$$\big[ 1+ (f')^2 \big] \ddot{x} + f' f''  \dot{x} ^2 + f'= 0 .$$

직선경로를 제외하면 운동방정식은 비선형이므로 mathematica의 $\tt NDSolve[]$을 이용해서 수치적으로 푼다.

(B) 원의 경우는 $x$ 좌표보다는 각변수를 이용하면 apparent singularity를 피할 수 있다. 이 경우 운동방정식은

$$ \ddot{\theta} = -\sin \theta,$$

로 주어진다. 

(C) cycloid는 곡선을 따라 움직이는 시간

$$t =\int \frac{ds}{v} = \int  \sqrt{\frac{1 + (dx/dy)^2}{2g(1-y)}}dy$$

을 최소로 만들어주는 곡선이다. cycloid는 다음과 같이 $R$ 변수와 각도 변수 $\theta$로 표현할 수 있다.

$$ 1-x=R(\theta-\sin \theta),~~y-1= -R(1-\cos \theta)$$

이 곡선이 $(0,0)$을 지나야 하는 조건에서 $R$과 그 때의 $\theta$ 값을 구할 수 있다. 먼저 $\theta$을 소거하면,

$$ R \cos \Big( \frac{1+\sqrt{2R-1}}{R} \Big) + 1 = R $$

을 얻고, 이 식의 근을 구하면 $R$ 값이 정해진다. 또한, $$1=R(\theta- \sin \theta)$$을 풀어서 $(0,0)$에 도달할 때 $\theta=\theta_0$ 값을 얻을 수 있다. 그리고 시간과 $\theta$ 변수의 관계는 위의 표현을 적분에 대입하면 

$$t = \sqrt{ \frac{R}{g} }  \theta $$

로 주어짐을 알 수 있다. 이는 사이클로이드가 일정하게 굴러가는 바퀴의 한 점이 그리는 자취이기 때문이다.

아래는 5가지 경우의 곡선 각각에서 운동을 보여주는 mathematica 코드다. 곡선의 모양에 따라 바닥에 도착하는 시간이 다름을 알 수 있다. 출발 높이가 $H$일 때 걸리는 시간은 $\sqrt{H/g}$ 단위로 

직선: $t_1=\int_0^1{ \frac{dy}{\sqrt{1-y}}} = 2$

2차 곡선: $t_2=\int_0^1\sqrt{ \frac{1+4y}{8y(1-y)}}dy= 1.86336$

6차 곡선: $t_6=\int_0^1 \sqrt{\frac{1+36y^{5/3}}{72y^{5/3}(1-y)}}dy=1.90954$

4분원: $t_c=\int_0^{\pi/2} \frac{d \theta}{\sqrt{2\sin \theta }}=1.85407$

cycloid: $t_0= \sqrt{R}\theta_0 = 1.82568$