Geometry & Recognition

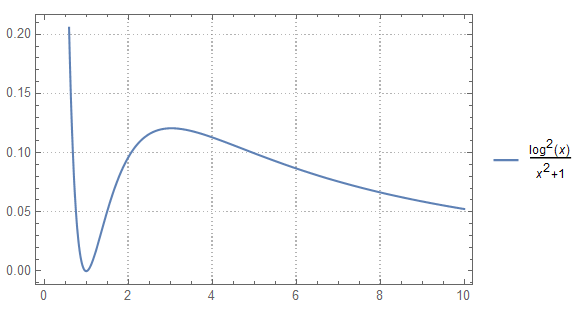
$$ I = \int_{-\infty}^\infty \frac{\log (1+x^4)dx}{1+x^2 }= \pi \log ( 6 + 4\sqrt{2})\approx 2.45589 \times \pi$$

복소평면에서 다음 $f(z)$의 contour 적분을 고려하자.

$$ f(z) = \frac{\log(1+z^4)}{1+z^2}$$

$z= \pm i$는 $f(z)$의 simple pole로 residue값은 각각 

$$ \text{Res} [f(\pm i)] =  \mp \frac{i}{2}\log 2 $$

그리고 $\log(1+z^4)$ 때문에 branch cut을 도입을 해야 하는데, branch point가

$$ z^4 +1 = 0~~\to ~~ z_k = e^{ i\frac{\pi}{4} (2k + 1)} , ~k=0,1,2,3$$

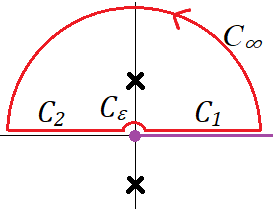
으로 주어지므로 그림과 같이 선택을 한다. 

\begin{align}\log(1+z^4) &= \sum_k \log(z-z_k)  \\ &= \sum_k \left[ \log|z- z_k| + i \text{arg}(z-z_k) \right] \\ &= \log|z^4 + 1| + i \sum _k A_k\end{align}

$k-$번째 cutline을 시계방향으로 건너면 $A_k$는 $2\pi$만큼 증가한다. 그림의 폐경로를 따라 적분을 하면

\begin{align} \oint f(z) dz &= \left(  \int_{C_\infty} + \int _{C_{0\epsilon}} + \int_{C_{1\epsilon}} + \int_{\gamma'_0} + \int _{\gamma_0}  +\int_{\gamma'_1 } + \int_{\gamma _1}  \right) f(z)dz + I \\ &= 2\pi i \times \text{Res}[f(+i)] \end{align}

인데,

$$ \int_{C_\infty} f(z)dz \to 0, ~~ \int_{C_{0\epsilon}} f(z) dz \to 0,~~ \int _{C_{1\epsilon}} f(z) dz \to 0$$ 

먼저 

\begin{align} \left(\int_{\gamma'_0 } + \int _{\gamma _0 } \right) f(z) dz &= -\int _{\gamma _0}  \frac{\log{|z^4 +1|}  + i (\frac{\pi}{4}+2\pi + A_1+ A_2 + A_3 ) }{1+z^2}dz    \\ & ~~~+ \int_{\gamma_0} \frac{\log |z^4 + 1| + i (\frac{\pi }{4} + A_1 +A_2 + A_3) }{1+z^2} dz \\ &=-2\pi i \int _{\gamma_0} \frac{dz}{1+z^2} \end{align}

마찬가지로 

$$\left( \int_{\gamma'_1} + \int_{\gamma_1}   \right) f(z) dz = -2\pi i \int _{\gamma_1} \frac{dz} {1+z^2}$$

이다. 그리고

$$ \int \frac{dz}{1+z^2} = \arctan(z) = \frac{1}{2i} \log \frac{1+i z}{1-iz}$$임을 이용하면 반직선 경로 $\gamma_0(\gamma_1)$를 따르는 적분은 하한 $z=z_0(z_1)$만 기여가 있다.

\begin{align} \int_{\gamma'_0+\gamma_0+ \gamma'_1+\gamma_1} f(z) dz & = \pi \log \left[ \frac{1+i e^{i\pi/4} } {1-i e^{i\pi/4}} \frac{1+i e^{i3\pi/4}}{1 - ie^{i3\pi/4}} \right] \\ &= \pi \log\frac{2-\sqrt{2}}{2+\sqrt{2}}\end{align} 

정리하면 

$$I  = \pi \log 2 - \pi \log \frac{2 - \sqrt{2}}{2 +\sqrt{2}} = \pi \log(6+ 4\sqrt{2})$$

$$ I = \int_0^\infty \frac{\log x  dx}{(1+x^2)^2}=-\frac{\pi}{4}$$

$\log$ 함수때문에 brach cut을 $-x$ 축으로 선택을 하고 ($-\pi < \text{arg}(z) \le \pi$) 함수 $f(z)$

$$ f(z) = \left( \frac{\log  z }{1+z^2}\right)^2$$

을 그림과 같은 열쇠 구멍 모양의 폐경로를 따라 적분하자.

폐경로가 double pole $z=\pm i$를 포함하므로

\begin{align} \left( \int_{C_1} + \int_{C_2} + \int_{C_{\epsilon}} + \int _{C_{\infty}} \right) f(z) dz &= -2\pi i \left[ \text{Res}f(z=i) + \text{Res}f(z=-i) \right]    \\ &=  -2\pi i \left( -\frac{\pi}{4} + i \frac{\pi^2}{16} -\frac{\pi}{4} - i \frac{\pi^2 }{16}\right) \\ &= i \pi^2 \end{align}

 여기서 

$$ \int_{C_\infty} f(z)dz \to 0,\quad \int_{C_\epsilon} f(z) dz \to 0$$

이고,  $C_1$ 경로는 $z= xe^{i\pi}, ~x:0\to\infty$이고, $C_2$ 경로는 $z=x e^{-i\pi}, ~x:\infty\to 0$이므로 

\begin{align} \int_{C_1} f(z) dz &=    \int_0^\infty \frac{(\log x +i \pi )^2  (-dx)}{(1+x^2)^2 } \\   &= -\int_0^\infty \frac{(\log x)^2 +2\pi i \log x -\pi^2 }{(1+x^2)^2}dx\end{align}

\begin{align} \int_{C_2} f(z)dz &= \int_\infty^0 \frac{(\log x -i \pi)^2 (-dx)}{(1+x^2)^2 } \\ &= \int_0^\infty \frac{(\log x)^2 - 2\pi i \log x -\pi^2}{(1+x^2)^2}dx\end{align}

이므로

$$  \left( \int_{C_1} + \int_{C_2} \right)f(z)dz = -4\pi i  \int_0^\infty \frac{\log x dx}{(1+x^2)^2 } $$

https://en.wikipedia.org/wiki/Contour_integration에 잘못된 내용이 들어감

$$I = \int_{0}^{\infty} \frac{(\log x)^2}{x^2 + 1}dx=\frac{\pi^3}{8}$$

복소평면에서 함수 $f(z) =\frac{(\log z)^2}{z^2 + 1}$를 고려하자. $z=0, \infty$가 $f(z)$의 두 branch point이므로 $+x$축을 cut line으로 선택하고 그림과 같은 contoure을 따라 적분을 하자. $z=\pm i$는 $f(z)$의 두 simple pole이다.

$C_\epsilon$에서 적분은 $z=\epsilon e^{i \theta},~\theta:\pi\to 0$로 표현하면 

$$ \int_{C_\epsilon} f(z)dz  = \int_\pi^0 {(\log \epsilon e^{i \theta} )^2}{i \epsilon e^{i \theta} d \theta } \to 0$$

마찬가지로 $\frac{(\log R)^2 }{ R} \to 0~(R\to \infty)$이므로 $C_\infty$에서 적분은 

$$\int_{C_\infty} f(z) dz = 0$$

$C_1$에서 적분은 $z=xe^{i0}, ~x:0\to \infty$이므로 

$$ \int_{C_1} f(z) dz = \int_0^\infty \frac{(\log x)^2}{x^2 + 1} dx= I$$

$C_2$에서 적분은 $z=xe^{\pi i}, ~x: \infty\to0$이므로( $\int_0^\infty \frac{\log x}{x^2+1}dx=0$)

\begin{align} \int_{C_2} f(z) dz &= \int _{\infty}^0 \frac{(\log x + \pi i )^2 }{x^2 + 1} e^{i \pi }dx \\ &= I + 2\pi i \int_\infty^0 \frac{\log x}  {x^2+1} e^{i\pi}dx -\pi^2 \int_\infty^0 \frac{dx}{x^2+1} e^{i\pi}dx \\   &= I + 0 - \frac{\pi^3}{2}\end{align}

Contour가 $z=i$ 포함하므로 residue 정리에 의해서 

$$ \int_{C_\epsilon + C_1 +C_2 +C_\infty} f(z)dz= 2\pi i \times \frac{(i\pi/2)^2}{2i}=-\frac{\pi^3}{4}$$

이므로 

$$ I = \int_0^\infty \frac { (\log x)^2 }{x^2+1} = \frac{\pi^3}{8}$$

$$I=\int_0^\infty \frac{dx}{1+x^4}$$

이 적분을 구하기 위해 $z=0$에 branch point를 가지는 복소함수

$$f(z)=\frac{\log  z }{1+z^4}$$

을 고려하자. Branch point가 $z=0, \infty$이므로 branch cut을 $+x$으로 선택하고 그림과 같은 contour에 대해서 $f(z)$를 적분을 한다.

$f(z)$는 $z=e^{i(2k+1) \pi/4}, ~(k=0,1,2,3)$에 simple pole을 가진다.

$$\oint_{C} f(z) dz = \left( \int_{C_1} + \int_{C_2} + \int_{C_R} + \int_{C_\epsilon} \right) f(z)dz.$$

$C_R$에 대한 적분은 $z=Re^{i\theta}$로 쓰면,

$$ \left| \int_{C_R} f(z) \right| =\left| \int_0^{2\pi} \frac{\log R + i \theta }{ 1 +R^4 e^{i4 \theta} } iR e^{i \theta} d \theta  \right| < (2\pi R) \frac{ \log  R + 2\pi }{R^4 -1} \rightarrow 0, \quad R \rightarrow \infty.$$ 

$C_\epsilon$에 대한 적분은 $z= \epsilon e^{i \theta}$로 쓰면

$$\left|  \int_{C_\epsilon} f(z) dz \right| = \left| \int_{2\pi}^0 \frac{ \log  \epsilon+ i \theta }{ 1+ \epsilon^4 e^{i 4\theta} } i \epsilon e^{i \theta } d \theta \right|  < (2\pi\epsilon) \frac{|\log \epsilon | + 2\pi }{1-\epsilon^4 } \rightarrow 0, \quad \epsilon \rightarrow 0  $$

$C_1$에서 $z=x e^{i0}, x: 0\rightarrow \infty$이고, $C_2$에서 $z= x e^{i 2\pi}, ~x: \infty \rightarrow 0$

$$ \int_{C_1 + C_2} f(z) dz = \int_0^\infty \frac{ \log x }{ 1+ x^4} dx + \int_\infty^0 \frac{\log x + i 2 \pi }{1+ x^4} dx = -i 2\pi \times I$$

Residue 정리에 의해서 

$$ \oint_{C} f(z)dz = 2\pi i \times  \sum_{k=0}^{3}\text{Res}(z=e^{i (2k+1) \pi/4}) = -i 2\pi \frac{\pi}{2\sqrt{2}}$$

이므로 

$$  I = \int_0^\infty \frac{dx}{1+x^4} = \frac{\pi}{2\sqrt{2}}$$

임을 확인할 수 있다.

아래는 Mathematica를 이용하여 얻은 결과다.

$$ I =  \text{Pr}\int_{-1}^1 \sqrt{ \frac{1+x}{1-x}} \frac{1}{(2-x)x} dx$$

복소함수 

$$f(z)=\left(\frac{1+z}{1-z} \right)^{1/2}\frac{1}{(2-z)z}$$

의 contour $\Gamma$에 대한 적분을 고려한다. $z=\pm1$이 branch point이고, $z=0,1$은 simple pole이다. cut line은 그림처럼 잡고, 위상은 $z=\pm 1$에서 $0\rightarrow 2\pi $로 선택한다.

residue 정리에 의해서 

$$ \int_\Gamma f(z) dz = 2i\pi \text{Res}(z=2) = \sqrt{3} \pi $$

$C_1$: $$\int_{C_1} f(z)dz = O(\sqrt{\epsilon}\epsilon)\rightarrow 0$$  

$C_5$: $$\int_{C_5} f(z)dz = O(\sqrt{\epsilon})\rightarrow 0$$  

$C_3$: $z=\epsilon e^{i \theta}~(\theta: \pi \rightarrow 2\pi)$, $z+1= e^{2i\pi}$, $z-1=e^{i\pi}$이므로

$$\int_{C_3} f(z) dz = \frac{e^{i\pi}}{e^{i\pi/2}e^{i\pi/2} } \int_{\pi}^{2\pi} \frac{i \epsilon e^{i\theta}}{2\epsilon e^{i \theta}} d\theta = i \frac{\pi}{2}.$$ 

$C_7$:  $z=e^{i\theta}~(\theta:0 \rightarrow \pi)$, $z+1 =e^{i 0}$, $z-1=e^{i \pi}$이므로

$$\int_{C_7} f(z) dz = \frac{1}{e^{i\pi/2}  e^{i\pi/2}}\int_0^\pi \frac{i\epsilon e^{i \theta}}{2\epsilon e^{i \theta}} d\theta =-i \frac{\pi}{2} $$

$C_2 + C_4$: $z+1= (x+1) e^{2i \pi }~(x: -1 \rightarrow +1)$, $z-1=(1-x)e^{i\pi}$이므로

$$\int_{C_2 + C_7} f(z)dz = \frac{e^{i\pi}}{e^{i\pi/2}e^{i\pi/2}}\int_{-1}^{1} \sqrt{\frac{1+x}{1-x}}\frac{dx}{(2-x)x}=I.$$

$C_6 + C_8$: $z+1= (x+1) e^{i 0}~(x: +1 \rightarrow -1)$, $z-1=(1-x)e^{i\pi}$이므로

$$\int_{C_2 + C_7} f(z)dz = \frac{1}{e^{i\pi/2}  e^{i\pi/2}}\int_{1}^{-1} \sqrt{\frac{1+x}{1-x}}\frac{dx}{(2-x)x}=I.$$

$C_\infty$: $$ \int_{C_\infty} f(z)dz = O( 1/R) \rightarrow0.$$

이 결과를 모두 정리하면,

$$ I =\text{Pr} \int_{-1}^1 \sqrt{\frac{1+x }{1-x}} \frac{dx}{(2-x)x}=\frac{\sqrt{3}}{2}\pi.$$