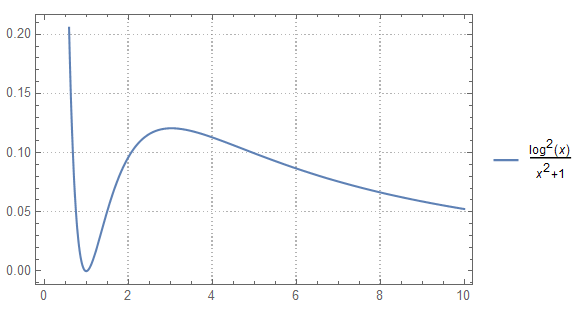
$$I = \int_{0}^{\infty} \frac{(\log x)^2}{x^2 + 1}dx=\frac{\pi^3}{8}$$
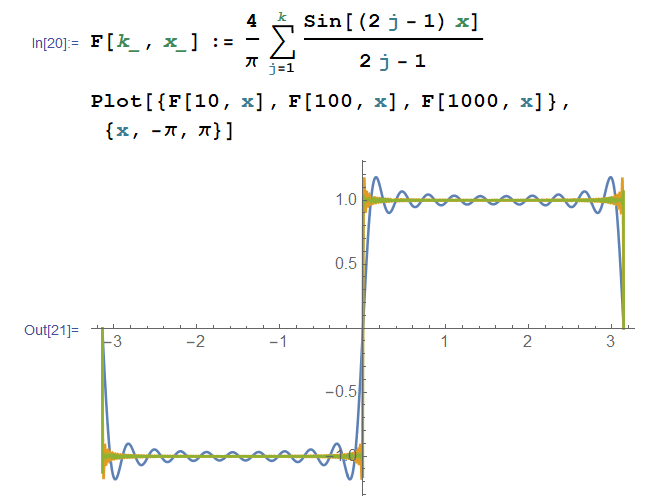
복소평면에서 함수 $f(z) =\frac{(\log z)^2}{z^2 + 1}$를 고려하자. $z=0, \infty$가 $f(z)$의 두 branch point이므로 $+x$축을 cut line으로 선택하고 그림과 같은 contoure을 따라 적분을 하자. $z=\pm i$는 $f(z)$의 두 simple pole이다.
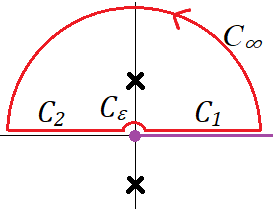
$C_\epsilon$에서 적분은 $z=\epsilon e^{i \theta},~\theta:\pi\to 0$로 표현하면
$$ \int_{C_\epsilon} f(z)dz = \int_\pi^0 {(\log \epsilon e^{i \theta} )^2}{i \epsilon e^{i \theta} d \theta } \to 0$$
마찬가지로 $\frac{(\log R)^2 }{ R} \to 0~(R\to \infty)$이므로 $C_\infty$에서 적분은
$$\int_{C_\infty} f(z) dz = 0$$
$C_1$에서 적분은 $z=xe^{i0}, ~x:0\to \infty$이므로
$$ \int_{C_1} f(z) dz = \int_0^\infty \frac{(\log x)^2}{x^2 + 1} dx= I$$
$C_2$에서 적분은 $z=xe^{\pi i}, ~x: \infty\to0$이므로( $\int_0^\infty \frac{\log x}{x^2+1}dx=0$)
\begin{align} \int_{C_2} f(z) dz &= \int _{\infty}^0 \frac{(\log x + \pi i )^2 }{x^2 + 1} e^{i \pi }dx \\ &= I + 2\pi i \int_\infty^0 \frac{\log x} {x^2+1} e^{i\pi}dx -\pi^2 \int_\infty^0 \frac{dx}{x^2+1} e^{i\pi}dx \\ &= I + 0 - \frac{\pi^3}{2}\end{align}
Contour가 $z=i$ 포함하므로 residue 정리에 의해서
$$ \int_{C_\epsilon + C_1 +C_2 +C_\infty} f(z)dz= 2\pi i \times \frac{(i\pi/2)^2}{2i}=-\frac{\pi^3}{4}$$
이므로
$$ I = \int_0^\infty \frac { (\log x)^2 }{x^2+1} = \frac{\pi^3}{8}$$
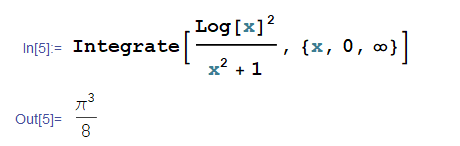
'Mathematics' 카테고리의 다른 글
| Tautochrone Curve(등시곡선) (0) | 2023.01.16 |
|---|---|
| Fourier transform of the Heviside step function (0) | 2023.01.12 |
| Gibbs Phenomenon (0) | 2022.05.06 |
| Catenary: Rolling Parabola (0) | 2022.02.03 |
| Catenary: rolling square wheels (0) | 2022.02.02 |