Geometry & Recognition

Fermat의 원리는 빛이 한 지점에서 다른 지점으로 진행할 때 가장 시간이 적게 드는 경로를 따라 움직인다고 이야기하고 있다. 광속은 굴절률이 큰 곳에서 작아지므로 굴절률이 다른 두 지점을 통과하는 빛의 경로는 되도록이면 광속이 큰 곳을 오래 머무르는 경로를 선택하는 것이 시간상 유리하다. 따라서 매질의 경계면에서 진행방향이 꺾여야 된다. 구체적으로 광속이 $v_1$인 매질에서 $v_2$인 매질로 빛이 진행할 때 입사각  $\alpha_1$,  굴절각 $\alpha_2$인 경우  

$$ \frac{ \sin \alpha_1 }{v_1}= \frac{\sin \alpha_2}{v_2} \quad \Longrightarrow \quad \frac{v} {\sin \alpha} =\text{const}$$을 만족한다. 여기서 $\alpha$는 빛의 진행 방향을 매질 경계면에 수직인 방향에 대해 잰 각이다.

Fermat의 원리는 중력장에서 움직이는 물체에 대해서도 적용할 수 있다. 물체가 움직이면 중력 때문에 속력이 변하게 되므로 두 지점을 잇는 직선을 따라 움직이는 경로는 최단시간 경로가 되지 못한다. 구체적으로 한 지점에서 출발해서 처음보다 아래방향으로 $y$만큼  속력은 역학적 에너지 보존에 의해서 

$$  v^2 = 2gy$$

로 주어진다. 속력이 $y$값이 (아래로) 증가하면 빨라지므로 굴절률이 $\sqrt{y}\sim \sqrt{-U_\text{grav}}$에 반비례해서 연속적으로 감소하는 경우로 생각할 수 있다. 

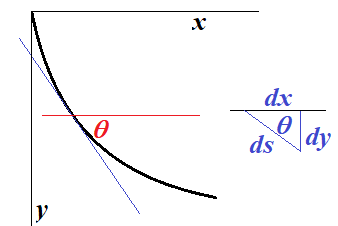
물체가 움직이는 경로상의 한 지점에서 접선이 수평에 대해 $\theta$만큼 기울어진 경우 입사각은 $\frac{\pi}{2}-\theta$이고, $\cos \theta = dx/ds$이다. 따라서 스넬의 법칙은 (제곱을 해서)

$$ \frac{v^2 }{ \sin ^2(\frac{\pi}{2}- \theta)} = \frac{v^2 }{\cos^2 \theta} = \frac{ 2gy}{(dx/ds)^2 } = \text{const} = 4gr$$

로 쓸 수 있다. $4gr$은 상수이다. 곡선의 미소길이

$$ ds =\sqrt{dx^2  + dy^2 } = \sqrt{1+(dy/dx)^2}dx$$

를 대입하면 중력장에서 물체가 움직이는 최소시간 경로는 다음의 비선형 미분방정식을 풀어서 얻을 수 있다.

$$ \Big( \frac{dy}{dx} \Big)^2 = \frac{2r}{y}-1\quad \Longrightarrow \quad dx = \sqrt{ \frac{y}{2r-y}}dy$$

잘 알려지다시피 이 방정식의 해는 cycloid 곡선으로 다음과 같이 표현할 수 있다. 

$$ x= r(\psi - \sin \psi ), \quad y = r (1- \cos \psi)$$

여기서 $\psi = {\pi-2\theta}$로 주어진다.

변분을 이용해서 구하는 경우는 https://kipl.tistory.com/186

수직 평면 상에서 곡선 $y=y(x)$을 따라 움직이는 물체의 운동을 생각하자. 이 물체는 마찰이 없이 움직일 수 있고 일정한 중력의 영향을 받는다. 높이 $y=h$에서 출발하여 바닥 $y=0$에 도달하는 데 걸리는 시간은 일반적으로 출발 높이에 따라 달라진다. 역학적 에너지 보존법칙을 쓰면 바닥까지 내려오는 데 걸리는 시간 $T(h)$는

$$ \frac{1}{2} \Big(\frac{d\ell}{dt}\Big)^2 + mgy = mgh \quad \Longrightarrow \quad T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{d \ell }{\sqrt{h-y}}$$

일반적으로 출발 높이가 낮으면 움직이는 거리가 짧아지므로 도착 시간도 짧아진다. 그러나 가속이 충분히 되지 않으므로 거리에 비례해서 시간이 짧아지지는 않는다. 그럼 도착 시간이 출발 높이에 무관하게 일정한 곡선을 찾을 수 있을까? 물론 답은 있고,  그때 물체가 움직이는 곡선을 tautochrone curve(등시곡선)이라 부른다.

물체가 움직이는 경로의 line element $d\ell $를 $$ d\ell = \sqrt{dx^2 +dy^2} = \sqrt{ 1 + \Big(\frac{dx}{dy}\Big)^2 } dy= f(y)dy$$처럼 쓰면 도착 시간은 $$T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{f(y)}{\sqrt{h-y}} dy$$

가 된다. 이는 $f(y)$와 $1/\sqrt{y}$의 convolution 형태가 되어 Laplace 변환을 사용하기 좋은 모양이다. 양변에 Laplace 변환을 취하면

\begin{align} \widetilde{T}(s) &= \frac{1}{\sqrt{2g}} \int_0^\infty \int_0^h \frac{f(y)}{\sqrt{h-y}} e^{-sh} dy dh\\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s){ \cal L}\Big[\frac{1}{\sqrt{h}}\Big](s) \\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s) \sqrt{\frac{\pi}{s}}  \end{align} 여기서  $ { \cal L}\left[\frac{1}{\sqrt{h}} \right] =\sqrt{\frac{\pi}{s}}$임을 이용했다 $\left(\int_0^\infty \frac{e^{-sh}}{\sqrt{h}}dh = 2 \int_0^\infty  {e^{-st^2}}dt = \sqrt{\frac{\pi}{s}}\right)$. 

도착 시간이 높이에 무관하게 일정하다면 $$T(h)= T_0=\text{const}$$로 쓸 수 있으므로 Laplace 변환은 $\widetilde{T}(s) = T_0/s$이다. 따라서 곡선 형태를 결정하는 $f(y)$의 Laplace 변환은

$$ \tilde{f}(s) = \sqrt{\frac{2gT_0^2}{\pi^2}} \sqrt{\frac{\pi}{s}}$$ 이를 역변환시키면 

$$ f(y) = \sqrt{\frac{2gT_0^2}{\pi^2}} \frac{1}{\sqrt{y}} $$임을 쉽게 알 수 있다. 이제 구체적인 곡선의 형태를 구하면 $$ x=\int dx =\int \sqrt{f^2(y)-1} dy =\int  \sqrt{ \frac{{2gT_0^2}/{\pi^2 } -  y}{y}}dy$$이고, 적분하기 위해 곡선이 $(x,y)=(0,0)$을 통과하는 조건을 주자. 그리고 $$y =  \frac{2gT_0^2}{\pi^2} \sin ^2( \theta/2) = \frac{gT_0^2}{\pi^2} (1- \cos \theta)$$로 매개변수화하면(이 경우 $dy/dx = \tan (\theta/2)$)

$$ x = \int_0^{ \theta_0}  \frac{ gT_0^2}{\pi^2} (1 +\cos \theta) d \theta \quad \Longrightarrow \quad x = \frac{gT_0^2}{\pi^2}( \theta + \sin \theta)$$

이어서 $(x(\theta), y(\theta))$는 cycloid가 됨을 알 수 있다. 이 cycloid는 반지름 $gT_0^2/\pi^2$인 원을 일정한 높이의 수평선 $y=2gT_0^2/\pi^2$에 접하게 굴릴 때 원점에서 바닥과 접촉했던 점이 그리는 곡선이고, $\theta$는 원의 중심과 이 점을 잇는 선분이 수직과 이루는 각을 나타낸다. 

위에서 구한 cycloid 곡선을 도착시간 공식에 대입해서 확인해 보자. 출발 높이가 $h$일 때 $h = \frac{gT_0^2}{\pi^2}( 1- \cos \theta_0)$로 놓으면 $$h-y= \frac{gT_0^2}{\pi^2} (\cos \theta - \cos \theta_0) \\ d\ell = \frac{gT_0^2 }{\pi^2}\sqrt{2(1+\cos \theta) } d \theta $$

이므로 내려가는데 걸리는 시간 \begin{align} T(h) & = \frac{T_0}{\pi} \int_0^{\theta_0} \sqrt{ \frac{1+\cos \theta}{ \cos \theta - \cos \theta_0 }} d \theta \\ &= \frac{2T_0}{\pi} \int_0^{\theta_0} {\frac{d\sin (\theta/2)}{\sqrt{\sin^2(\theta_0/2)-\sin^2(\theta/2)}}}= T_0 \end{align}이 출발 높이($=h$)에 상관없이 일정함을 확인할 수 있다. 바닥까지 내려가는데 걸리는 시간 $T_0$가 정해지면 원의 반지름 $gT_0^2/\pi$이 결정되어 곡선 모양이 자동으로 정해진다.

https://youtu.be/Ib1TdgeYL4o

Cycloid는 이 성질 이외에도 일정한 중력하에서 두 지점을  연결하는 곡선을 움직일 때 최단 시간을 주는 곡선이기도 하다(brachistochrone curve) 

https://kipl.tistory.com/186

Heviside step function $\theta(t)$은 높이가 1인 계단형 함수로 다음과 같이 정의된다.

$$ \theta (t) = \left\{ \begin{matrix}  1 & t\ge 0  \\ 0 & t <0\end{matrix}\right.$$

이 함수의 fourier transform을 구하려 할 때 이 정의 그대로 대입해서는 올바른 결과를 얻을 수 없다. 이를 위해서 $\theta$를 미분하면 delta 함수를 얻을 수 있고, $\delta (t)$를 다음과 같은 Fourier transform 형태로 쓸 수 있음을 이용하자.

$$ \delta (t) = \frac{1}{2 \pi} \int_{-\infty}^\infty e^{- i \omega t} d \omega = \frac{d}{dt} \theta(t) $$ 따라서 적분을 해서 다음과 같이 생각할 수 있다.

$$\theta (t)  \overset{?}{=} \frac{i}{2\pi }  \int_{-\infty}^\infty \frac{e^{-i \omega t}}{ \omega} d \omega$$

그러나 이 적분은 $\omega=0$에서 제대로 정의가 안되므로 이를 회피하는 방법을 고안해야 한다. 이를 위해서 복소평면으로 확장을 한 후 pole의 위치를  $\omega=0$에서 조금 이동해서 $\omega = - i\epsilon~(\epsilon \to 0^+)$이 되도록 하자. 물론 $\omega = +i \epsilon$ 쪽으로도 옮기는 경우도 고려할 수 있지만 이 경우에는 $\theta(-t)$가 된다. 이제 확인해 보도록 하자: $$ \boxed{\theta(t) = \lim_{\epsilon\to 0^+} \frac{i}{2\pi} \int_{-\infty}^\infty \frac{e^{-i \omega t}}{\omega +i \epsilon} d\omega}$$

$t>0$인 경우는 복소평면의 아랫부분을 시계방향으로 도는 경로를 잡아서 적분하면 원호 부분에서는 기여가 없고 residue 정리에 의해서

$$ \frac{i}{2\pi} \oint_\text{lower half} \frac{e^{-i\omega t}}{\omega+i \epsilon}d \omega = (-2\pi i) \frac{i}{2\pi}e^{-it (-i\epsilon)} = e^{- \epsilon t}$$ 

$t<0$일 때는 복소평면 위쪽을 반시계방향으로 회전하는 경로를 잡아서 적분하면 

$$ \frac{i}{2\pi} \oint_\text{upper half} \frac{e^{-i\omega t}}{\omega+i \epsilon}d \omega = 0$$

정리하면 $$  \theta (t) = \lim_{ \epsilon\to 0^+}\left\{ \begin{matrix}   e^{-\epsilon t} & t \ge 0 \\ 0 & t < 0  \end{matrix}\right. $$

따라서 위의 적분이 제대로 된 $\theta(t)$의 한 표현을 제공함을 확인할 수 있다(Note, for $\epsilon>0$, $ \int_{-\infty}^\infty |\theta_\epsilon (t)| < \infty$이어서  Dirichlet condition을 만족시킴). 그런데 이 적분 표현은 Fourier transform의 형태를 가지므로 $\theta(t)$의 Fourier transform 역변환 정의 $$\theta(t)=\frac{1}{2\pi}\int \tilde{\theta}(\omega)e^{-i\omega t} d\omega$$와 비교하면

\begin{gather} \tilde { \theta}(\omega) =  \lim_{\epsilon\to 0^+ }\frac{i}{\omega + i \epsilon}   =\lim_{\epsilon\to0^+} \frac{ \epsilon+ i \omega}{\omega^2 + \epsilon^2}   =  \lim_{\epsilon\to0^+} \frac{\epsilon}{\omega^2 + \epsilon^2 } - \frac{1}{i\omega}   \\ \text{or} \\ {\tilde{\theta}(\omega) = \pi \delta (\omega) - \frac{1}{i \omega} } \end{gather}을 얻는다. 여기서 Lorentzian를 이용한 delta 함수를 표현을 사용했다. 그리고 $1/\omega$ 부분의 적분은 Cauchy의 pricipal value prescription을 써서 적분을 해야 한다. \begin{align} \frac{1}{2\pi} \text{P} \int_{-\infty}^\infty \frac{1}{-i\omega} g(\omega)d\omega &=\frac{1}{2\pi} \lim_{\delta \to 0} \left( \int_{-\infty}^{-\delta} + \int_\delta ^\infty  \right) \frac{1}{- i\omega} g(\omega)d\omega\end{align}

$$ \boxed{\tilde{\theta}(\omega) = \pi \delta (\omega) - \text{P} \left( \frac{1}{i \omega} \right) }$$

시간 변수에 대한 역 Fourier transform의 정의로 $$ f(t) = \frac{1}{2\pi} \int_{-\infty}^\infty  {\tilde f}(\omega) e^{i \omega t} d \omega$$

을 사용하는 경우에는 앞의 결과에서 $\omega \to - \omega$를 해서, $$ \tilde{\theta}(\omega) = \pi \delta(\omega) + \frac{1}{i \omega}$$가 된다. 물리적으로는 에너지 연산자가 $i\hbar \partial/\partial t$이므로 시간 변수의 Fourier 변환은 전자의 정의를 사용하고, 운동량 연산자가 $-i \hbar \nabla$이므로 공간 변수에 대한 Fourier 변환은 후자를 사용한다.