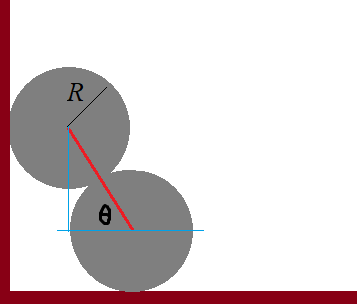
두 개의 동일한 실린더 그림과 같이 쌓여 있다. 밑에 있는 실린더에 오른쪽으로 살짝 충격을 주어 움직이게 만든다. 아래 실린더가 가질 수 있는 최대속력은? 바닥, 벽, 실린더 사이의 마찰은 무시할 수 있다.

풀이:
마찰이 없으므로 실린더의 회전운동은 없고, 위 실린더는 아래로 내려가는 운동을, 아래 실린더는 수평운동만 한다. 두 실린더가 접촉을 하는 동안 위쪽 실린더의 중심 높이를 $y$, 내려가는 속력은 $v_y$, 아래쪽 실린더의 수평위치를 $x$, 수평속도를 $v_x$, 그리고 두 실린더의 중심을 연결하는 선분이 수평과 이루는 각을 $\theta$라면
$$ x= R + 2R \cos \theta,~~~y = R+2R \sin \theta $$
$$ v_x = -2R \sin \theta \frac{d \theta }{dt} ,~~~v_y = 2R \cos \theta \frac{d \theta}{dt} $$
역학적에너지 보존을 이용하면
$$ \frac{1}{2} M (v_x^2 + v_y^2) = 2MgR(1-\sin \theta) $$
$$ \to~~ v_x^2 + v_y^2 = 4gR(1-\sin \theta) $$
$$ \to~~ \left( \frac{d \theta}{dt}\right) ^2 = \frac{g}{R} (1-\sin \theta) $$
$$ \therefore ~ v_x^2 = 4Rg (\sin^2 \theta - \sin^3 \theta) $$
따라서
$$\frac{dv_x^2}{dt} = 4Rg \cos \theta ( 2 \sin \theta - 3 \sin ^2 \theta) \frac{d \theta}{dt}= 2 v_x \frac{dv_x}{dt} $$
$$ \to ~~ \frac{dv_x}{dt} = g\cos \theta (3\sin \theta-2)$$이므로 $$ \sin\theta = \frac{2}{3}$$
일 때 최댓값에 도달한다.
$$ (v_x)_\text{max} = \frac{4}{3\sqrt{3}} \sqrt{Rg}$$
아래쪽 실린더는 위쪽 실린더가 접촉면에서 누르는 힘($\vec{R}$)의 수평성분에 의해 가속이 되는데 $\theta =\sin^{-1} (2/3)$에서 두 실린더의 접촉이 없어지므로 수평성분의 변화가 생기지 않는다.
$$ R_x = M \frac{dv_x}{dt} = Mg \cos \theta ( 3\sin \theta-2)$$
윗쪽 실린더에 대해서도 확인하면,
$$ v_y^2 = 4Rg \cos^2 \theta ( 1- \sin \theta) $$
$$ M \frac{dv_y}{dt} = -Mg +R_y $$
$$ \to ~~ R_y = Mg + M \frac{dv_y}{dt} = Mg \sin \theta ( 3 \sin \theta - 2)$$어서 $R_y$도 0이 됨을 알 수 있다.
'Physics > 역학' 카테고리의 다른 글
| 손에 충격을 덜 받으면서 나무 부러뜨리기 (0) | 2025.01.05 |
|---|---|
| 링이 위로 튈 수 있는 조건은? (4) | 2025.01.04 |
| 미끄러지지 않을 조건은? (0) | 2025.01.03 |
| 체인이 움직이는 속력은? (1) | 2025.01.02 |
| 막대진자의 최소 진동 주기는? (0) | 2024.12.31 |




