Geometry & Recognition

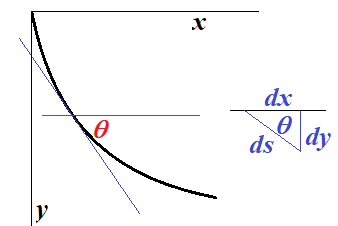
인간 눈의 시야각은 180도를 넘기 때문에 지상에서 하늘을 보면 (시야를 가리는 방해물이 없다면) 무한히 넗게 보인다. 그럼 잔잔한 호수에 잠수해서 하늘을 쳐다보면 어떻게 보일까? 우리가 물체를 본다는 것은 그 물체에서 나오거나 반사된 빛이 우리 눈으로 들어옴을 의미한다. 그런데 공기 중에서 직선으로 진행하던 빛이 물속으로 들어오면 경로가 꺾이게 된다. 이는 Snell의 법칙으로 기술이 되는데 수면에 수직한 방향에 대해서 $\theta_\text{air}$으로 공기 중에서 물속으로 들어오는 빛은 $\theta_\text{water}$만큼 꺾여서 물속에서 진행하는데, 물의 굴절률을 $n_\text{water}$라 하면 수식으로는 

$$ \sin \theta_\text{air} = n_\text{water} \sin \theta_\text{water}$$으로 표현된다. 물의 굴절률이 $n_\text{water}\approx 1.333$ 정도 이므로 하늘에서 다양한 각도로 수면에 입사해서 사람의 눈에 들어오는 빛을 생각해 보면 항상 $\theta_\text{water} < \theta_\text{air}$임으로 알 수 있다. 특히 수면에 거의 나란하게 들어오는 빛($\theta_\text{air}=90^\circ$)은 물속에서는 

$$ \theta_\text{water} = \sin^{-1} \frac{1}{n_\text{water}} \approx 49^\circ$$로 들어오는 것으로 보인다.

사람은 자신의 눈에 들어오는 빛의 방향으로 물체의 위치를 파악하므로 물속에서는 하늘과 지상의 경계가 마치 자신의 눈에는 $49^\circ$에 있는 것으로 인식하게 된다. 호수가 충분히 넓다면 모든 방향의 수면에 나란하게 들어오는 빛은 $49^\circ$로 들어오는 것으로 인식하므로 물속에서는 하늘이 둥근 원안에 있는 것으로 보이게 된다. 그 각도 바깥은 수면에서 전반사 현상에 의해서 (충분히 맑은 물이라면) 호수 내부의 모습이 보이게 된다. 눈이 수면에서 $d$만큼 아래에 있다면 하늘은 반지름이

$$ R \approx   d \tan 49^\circ$$

인 원 내부에 있는 것으로 보일 것이다. 역설적이게도 수면에 가까이 있을수록 하늘이 더 작게 보인다.

Fermat의 원리는 빛이 한 지점에서 다른 지점으로 진행할 때 가장 시간이 적게 드는 경로를 따라 움직인다고 이야기하고 있다. 광속은 굴절률이 큰 곳에서 작아지므로 굴절률이 다른 두 지점을 통과하는 빛의 경로는 되도록이면 광속이 큰 곳을 오래 머무르는 경로를 선택하는 것이 시간상 유리하다. 따라서 매질의 경계면에서 진행방향이 꺾여야 된다. 구체적으로 광속이 $v_1$인 매질에서 $v_2$인 매질로 빛이 진행할 때 입사각  $\alpha_1$,  굴절각 $\alpha_2$인 경우  

$$ \frac{ \sin \alpha_1 }{v_1}= \frac{\sin \alpha_2}{v_2} \quad \Longrightarrow \quad \frac{v} {\sin \alpha} =\text{const}$$을 만족한다. 여기서 $\alpha$는 빛의 진행 방향을 매질 경계면에 수직인 방향에 대해 잰 각이다.

Fermat의 원리는 중력장에서 움직이는 물체에 대해서도 적용할 수 있다. 물체가 움직이면 중력 때문에 속력이 변하게 되므로 두 지점을 잇는 직선을 따라 움직이는 경로는 최단시간 경로가 되지 못한다. 구체적으로 한 지점에서 출발해서 처음보다 아래방향으로 $y$만큼  속력은 역학적 에너지 보존에 의해서 

$$  v^2 = 2gy$$

로 주어진다. 속력이 $y$값이 (아래로) 증가하면 빨라지므로 굴절률이 $\sqrt{y}\sim \sqrt{-U_\text{grav}}$에 반비례해서 연속적으로 감소하는 경우로 생각할 수 있다. 

물체가 움직이는 경로상의 한 지점에서 접선이 수평에 대해 $\theta$만큼 기울어진 경우 입사각은 $\frac{\pi}{2}-\theta$이고, $\cos \theta = dx/ds$이다. 따라서 스넬의 법칙은 (제곱을 해서)

$$ \frac{v^2 }{ \sin ^2(\frac{\pi}{2}- \theta)} = \frac{v^2 }{\cos^2 \theta} = \frac{ 2gy}{(dx/ds)^2 } = \text{const} = 4gr$$

로 쓸 수 있다. $4gr$은 상수이다. 곡선의 미소길이

$$ ds =\sqrt{dx^2  + dy^2 } = \sqrt{1+(dy/dx)^2}dx$$

를 대입하면 중력장에서 물체가 움직이는 최소시간 경로는 다음의 비선형 미분방정식을 풀어서 얻을 수 있다.

$$ \Big( \frac{dy}{dx} \Big)^2 = \frac{2r}{y}-1\quad \Longrightarrow \quad dx = \sqrt{ \frac{y}{2r-y}}dy$$

잘 알려지다시피 이 방정식의 해는 cycloid 곡선으로 다음과 같이 표현할 수 있다. 

$$ x= r(\psi - \sin \psi ), \quad y = r (1- \cos \psi)$$

여기서 $\psi = {\pi-2\theta}$로 주어진다.

변분을 이용해서 구하는 경우는 https://kipl.tistory.com/186

깊이가 $h$ 인 수영장 바닥에 있는 물체를 물 밖에서 바라볼 때 얼마의 깊이에 있는 것으로 보일까? 단, 바라보는 각도는 수직에 대해서 $\theta$ 이고, 물의 굴절률은 $n$ 이다. 참고: 그림은 물체의 위가 겉보기 위치인 것처럼 그려졌으나 항상 그런 것은 아니다.

1. $\frac{h}{n} \Big(  \frac{\cos^2 \theta}{1-{\sin^2 \theta}/{n^2} } \Big)^{3/2}$ 

2. $\frac{h}{n}$

3. $\frac{h\cos\theta}{n}$

더보기

 

눈은 작지만 유한한 크기를 가지고 있으므로 물체의 한 점에서는 나오는 여러 광선을 받아들인다. 눈에 들어오는 광선들의 연장선이 만나는 지점에 물체의 겉보기 위치가 된다. 그리고 같이 광선 1과 2의 경로를 분석해보자. 눈이 작으므로 두 광선은 매우 가까이 있다( $\delta\ll 1$: 그림은 과장되게 그려진 것이다). 광선 1에 Snell의 법칙을 적용하면

$$ n \sin\theta_i = \sin \theta_r$$

이다. 이보다 조금 다른 각도 $(\theta_r + d\theta_r)$ 로 들어오는 광선 2에 대해서도 Snell의 법칙을 적용한 후 $((n \sin (\theta_i + d\theta_i)  = \sin(\theta_r +d\theta_r) )$ 광선 1과의 차이를 구하면

$$ n \cos\theta_i d\theta_i  =\cos \theta_r d \theta_r  \quad \rightarrow \quad \frac{d\theta_i}{d\theta_r} = \frac{\cos\theta_r}{n\cos \theta_i}$$

그림에서 광선 1의 실제 경로에 대해서 물체의 수평 거리$(x)$와 깊이$(y)$의 관계는  $x=y\tan \theta_i$, 광선 2에 대해서는 $x+\delta = y \tan(\theta_i + d\theta_i)$이므로 둘의 차이를 계산하면

$$ \delta = y \sec^2 \theta_i d \theta_i$$

마찬가지로 광선1 과 2의 겉보기 경로에 대해 겉보기 수평 거리$(x_a)$와 깊이$(y_a)$의 관계를 정리하면

$$\delta = y_a \sec^2\theta_r d \theta_r$$

이므로

$$ \frac{d\theta_i}{d\theta_r} = \frac{y_a \cos^2 \theta_i}{y \cos^2 \theta_r}$$

두 결과를 종합하면

$$ y_a = \frac{y}{n} \left( \frac{\cos \theta_r}{\cos \theta_i}\right)^3 = \frac{y}{n}\left( \frac{\cos^2 \theta_r}{1 - {\sin^2 \theta_r}/{n^2}}\right)^{3/2}$$