Geometry & Recognition

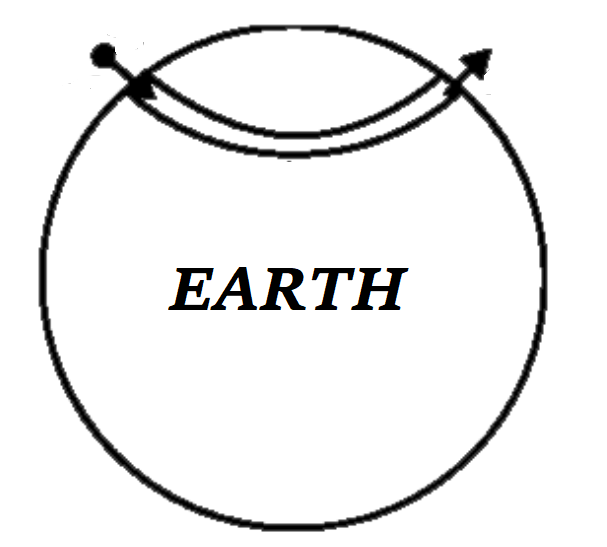
지구 내부(물론 지구는 완벽한 반지름 $R$인 구이고 밀도는 균일하다고 가정한다)에 직선 터널을 뚫어 두 지점을 연결할 때 순수한 중력에 의해서 터널을 통과하는 데 걸리는 시간은 직선 터널의 길이에 상관없이 항상 $T= \pi \sqrt{\frac{R}{g}}=42~\text{min}$로 주어진다. 이는 지표면을 스치듯이 지나는 인공위성의 주기의 절반에 해당한다. 균일한 중력장에서 두 지점을 잇는 직선 경로가 최단 시간 경로가 아니듯 이 경우에도 더 짧은 통과시간을 가지는 경로를 만들 수 있다.

우선 지구 내부에서 질량 $m$인 물체에 작용하는 중력의 세기는 가우스 법칙을 쓰면

$$ \vec{F} =-\frac{GM m} {R^3} \vec {r}= -k \vec{r} = -m \omega^2 \vec{r}, \quad \omega^2 = \frac{GM}{R^3} = \frac{g}{R}$$

처럼 쓸 수 있다(용수철의 탄성력과 같다). 그리고 보존력이므로 위치에너지 함수를 가지는데

$$U(\vec{r}) = \frac{1}{2} m\omega^2 r^2$$

이고 역학적 에너지는 보존된다. 지표면에서 출발을 하면 역학적 에너지는

$$ E= K+U =\frac{1}{2} mv^2 + \frac{1}{2} m \omega^2 r^2 = \frac{1}{2} m \omega^2 R^2 $$

따라서 중심에서 $r$만큼 떨어진 지점에서 물체의 속력은

$$  v= \omega \sqrt{R^2 - r^2}$$

그리고 주어진 터널을 지나는 데 걸리는 시간은

$$ t = \int \frac{d\ell }{v} = \frac{1}{\omega}\int \frac{d\ell }{ \sqrt{R^2-r^2}}$$

터널은 항상 출발, 지구 중심, 도착 지점을 포함하는 한 평면 상에 있어야 하므로 평면 극좌표 $(r, \theta)$를 사용하는 것이 편리하다. 이 경우 터널 곡선은 $r = r(\theta)$로 표현할 수 있으므로

$$ d\ell  = \sqrt{(dr)^2 + (r d\theta)^2} = \sqrt{ r^2 + \dot{r}^2 } d \theta$$

여기서 $\dot{r}= dr/d\theta$를 나타낸다. 터널 통과시간은 따라서

$$ t= \frac{1}{ \omega} \int \sqrt{ \frac{r^2 + \dot{r}^2 }{R^2 - r^2}} d\theta$$

최단 시간을 주는 터널 모양을 찾는 문제는 $t$을 최소시키는 $r(\theta)$를 찾는 변분문제가 된다. 적분인자가 $\theta$에 명시적으로 의존하지 않으므로 Euler-Lagrange 방정식을 써서 

$$ \frac{r^2}{\sqrt{(R^2 - r^2 ) (r^2 + \dot{r}^2)}}=\frac{1}{C} = \text{const} \\ \Longrightarrow \quad \dot{r}^2 = \frac{r^2[(1+C^2)r^2-R^2 ]}{R^2-r^2}$$

임을 보일 수 있다. 중심에서 가장 가까이 왔을 때($\dot r=0$) 거리를 $R_0$라면, $(1+C^2) R_0^2 =R^2$이므로

$$\dot{r}^2 = \frac{r^2\left(\frac{R^2}{R_0^2} r^2-R^2 \right)}{R^2-r^2}$$

모든 거리를 $R$ 단위로 재면 (이 경우 반지름이 1인 행성에서의 터널 문제가 된다) 터널 곡선은 다음 미분방정식을 풀어서 얻을 수 있다.

$$ s = r/R,~~ s_0 = R_0/R, $$

$$ \frac{d s}{d \theta} = \pm \frac{s}{s_0} \sqrt{\frac{s^2 - s_0^2 }{ 1-s^2}}$$

$$ \Longrightarrow ~~\theta = -\int   \frac{s_0}{s} \sqrt{\frac{1-s^2}{s^2 - s_0^2 }}ds $$

적분인자의 root를 벗기기 위해서

$$s^2 = \cos^2 \frac{\phi}{2} + s_0^2 \sin ^2 \frac{\phi}{2}$$로 치환하면 

$$ \theta = s_0 (1-s_0^2) \int \frac{\sin^2 \frac{\phi}{2}}{\cos^2 \frac{\phi}{2}+s_0^2 \sin^2\frac{\phi}{2} }d \frac{\phi}{2} $$

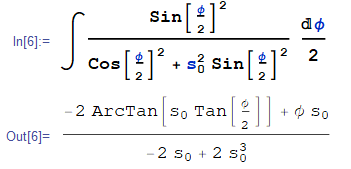
$$\Longrightarrow\quad \theta = \tan^{-1} \left( s_0 \tan \frac{\phi}{2}\right) -\frac{s_0}{2} \phi$$

를 얻는다. 출발지점은 $\phi=0$이고, 중심에서 가장 가까운 지점$(r=R_0)$은 $\phi=\pi$ 그리고 도착지점은 $\phi=2\pi$에 해당한다. 이제 도착시간을 계산하면 

$$t = \frac{1}{\omega} \int  \frac{sds}{\sqrt{(1-s^2) (s^2- s_0^2) }} $$로 쓸 수 있는데 앞의 치환을 이용하면 

$$  t = \frac{1}{2\omega} \sqrt{1- s_0^2} \phi$$

를 얻는다. $\phi= 2\pi$을 대입하면 

$$ t ={\pi}\sqrt{\frac{R}{g}} \sqrt{1-  \left(\frac{R_0}{R}\right)^2}$$

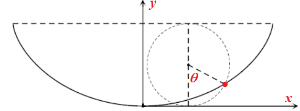
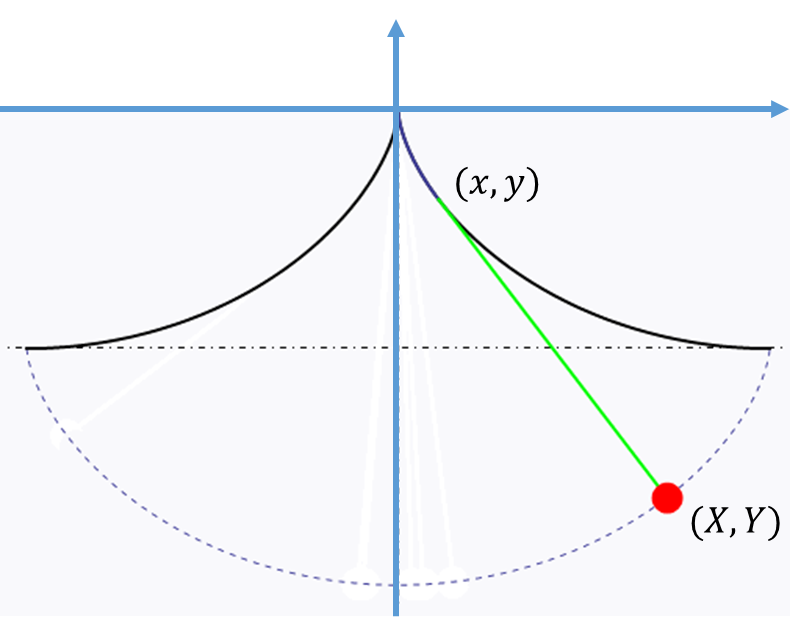
이어서 직선 터널을 움직이는 시간보다 짧다. 그리고 중심을 통과할 때는 ($R_0=0$) 곡선은 직선이 된다. 지구 내부에서 최단시간 곡선은 지구 내부에서 반지름 $r= (R-R_0)/2$인 원을 굴렸을 때 원의 한 지점이 그리는 곡선의 자취로 표현되고, 이 곡선을 hypocycloid라 한다. 이는 직교좌표를 사용하면 더 쉽게 볼 수 있다.

--계속--

Fermat의 원리는 빛이 한 지점에서 다른 지점으로 진행할 때 가장 시간이 적게 드는 경로를 따라 움직인다고 이야기하고 있다. 광속은 굴절률이 큰 곳에서 작아지므로 굴절률이 다른 두 지점을 통과하는 빛의 경로는 되도록이면 광속이 큰 곳을 오래 머무르는 경로를 선택하는 것이 시간상 유리하다. 따라서 매질의 경계면에서 진행방향이 꺾여야 된다. 구체적으로 광속이 $v_1$인 매질에서 $v_2$인 매질로 빛이 진행할 때 입사각  $\alpha_1$,  굴절각 $\alpha_2$인 경우  

$$ \frac{ \sin \alpha_1 }{v_1}= \frac{\sin \alpha_2}{v_2} \quad \Longrightarrow \quad \frac{v} {\sin \alpha} =\text{const}$$을 만족한다. 여기서 $\alpha$는 빛의 진행 방향을 매질 경계면에 수직인 방향에 대해 잰 각이다.

Fermat의 원리는 중력장에서 움직이는 물체에 대해서도 적용할 수 있다. 물체가 움직이면 중력 때문에 속력이 변하게 되므로 두 지점을 잇는 직선을 따라 움직이는 경로는 최단시간 경로가 되지 못한다. 구체적으로 한 지점에서 출발해서 처음보다 아래방향으로 $y$만큼  속력은 역학적 에너지 보존에 의해서 

$$  v^2 = 2gy$$

로 주어진다. 속력이 $y$값이 (아래로) 증가하면 빨라지므로 굴절률이 $\sqrt{y}\sim \sqrt{-U_\text{grav}}$에 반비례해서 연속적으로 감소하는 경우로 생각할 수 있다. 

물체가 움직이는 경로상의 한 지점에서 접선이 수평에 대해 $\theta$만큼 기울어진 경우 입사각은 $\frac{\pi}{2}-\theta$이고, $\cos \theta = dx/ds$이다. 따라서 스넬의 법칙은 (제곱을 해서)

$$ \frac{v^2 }{ \sin ^2(\frac{\pi}{2}- \theta)} = \frac{v^2 }{\cos^2 \theta} = \frac{ 2gy}{(dx/ds)^2 } = \text{const} = 4gr$$

로 쓸 수 있다. $4gr$은 상수이다. 곡선의 미소길이

$$ ds =\sqrt{dx^2  + dy^2 } = \sqrt{1+(dy/dx)^2}dx$$

를 대입하면 중력장에서 물체가 움직이는 최소시간 경로는 다음의 비선형 미분방정식을 풀어서 얻을 수 있다.

$$ \Big( \frac{dy}{dx} \Big)^2 = \frac{2r}{y}-1\quad \Longrightarrow \quad dx = \sqrt{ \frac{y}{2r-y}}dy$$

잘 알려지다시피 이 방정식의 해는 cycloid 곡선으로 다음과 같이 표현할 수 있다. 

$$ x= r(\psi - \sin \psi ), \quad y = r (1- \cos \psi)$$

여기서 $\psi = {\pi-2\theta}$로 주어진다.

변분을 이용해서 구하는 경우는 https://kipl.tistory.com/186

수직 평면 상에서 곡선 $y=y(x)$을 따라 움직이는 물체의 운동을 생각하자. 이 물체는 마찰이 없이 움직일 수 있고 일정한 중력의 영향을 받는다. 높이 $y=h$에서 출발하여 바닥 $y=0$에 도달하는 데 걸리는 시간은 일반적으로 출발 높이에 따라 달라진다. 역학적 에너지 보존법칙을 쓰면 바닥까지 내려오는 데 걸리는 시간 $T(h)$는

$$ \frac{1}{2} \Big(\frac{d\ell}{dt}\Big)^2 + mgy = mgh \quad \Longrightarrow \quad T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{d \ell }{\sqrt{h-y}}$$

일반적으로 출발 높이가 낮으면 움직이는 거리가 짧아지므로 도착 시간도 짧아진다. 그러나 가속이 충분히 되지 않으므로 거리에 비례해서 시간이 짧아지지는 않는다. 그럼 도착 시간이 출발 높이에 무관하게 일정한 곡선을 찾을 수 있을까? 물론 답은 있고,  그때 물체가 움직이는 곡선을 tautochrone curve(등시곡선)이라 부른다.

물체가 움직이는 경로의 line element $d\ell $를 $$ d\ell = \sqrt{dx^2 +dy^2} = \sqrt{ 1 + \Big(\frac{dx}{dy}\Big)^2 } dy= f(y)dy$$처럼 쓰면 도착 시간은 $$T(h) = \frac{1}{\sqrt{2g}} \int_0^h \frac{f(y)}{\sqrt{h-y}} dy$$

가 된다. 이는 $f(y)$외 $1/\sqrt{y}$의 convolution 형태가 되어 Laplace 변환을 사용하기 좋은 모양이다. 양변에 Laplace 변환을 취하면

\begin{align} \widetilde{T}(s) &= \frac{1}{\sqrt{2g}} \int_0^\infty \int_0^h \frac{f(y)}{\sqrt{h-y}} e^{-sh} dy dh\\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s){ \cal L}\Big[\frac{1}{\sqrt{h}}\Big](s) \\ &=\frac{1}{\sqrt{2g}} \tilde{f}(s) \sqrt{\frac{\pi}{s}}  \end{align} 여기서  $ { \cal L}\left[\frac{1}{\sqrt{h}} \right] =\sqrt{\frac{\pi}{s}}$임을 이용했다 $\left(\int_0^\infty \frac{e^{-sh}}{\sqrt{h}}dh = 2 \int_0^\infty  {e^{-st^2}}dt = \sqrt{\frac{\pi}{s}}\right)$. 

도착 시간이 높이에 무관하게 일정하다면 $$T(h)= T_0=\text{const}$$로 쓸 수 있으므로 Laplace 변환은 $\widetilde{T}(s) = T_0/s$이다. 따라서 곡선 형태를 결정하는 $f(y)$의 Laplace 변환은

$$ \tilde{f}(s) = \sqrt{\frac{2gT_0^2}{\pi^2}} \sqrt{\frac{\pi}{s}}$$ 이를 역변환시키면 

$$ f(y) = \sqrt{\frac{2gT_0^2}{\pi^2}} \frac{1}{\sqrt{y}} $$임을 쉽게 알 수 있다. 이제 구체적인 곡선의 형태를 구하면 $$ x=\int dx =\int \sqrt{f^2(y)-1} dy =\int  \sqrt{ \frac{{2gT_0^2}/{\pi^2 } -  y}{y}}dy$$이고, 적분하기 위해 곡선이 $(x,y)=(0,0)$을 통과하는 조건을 주자. 그리고 $$y =  \frac{2gT_0^2}{\pi^2} \sin ^2( \theta/2) = \frac{gT_0^2}{\pi^2} (1- \cos \theta)$$로 매개변수화하면(이 경우 $dy/dx = \tan (\theta/2)$)

$$ x = \int_0^{ \theta_0}  \frac{ gT_0^2}{\pi^2} (1 +\cos \theta) d \theta \quad \Longrightarrow \quad x = \frac{gT_0^2}{\pi^2}( \theta + \sin \theta)$$

이어서 $(x(\theta), y(\theta))$는 cycloid가 됨을 알 수 있다. 이 cycloid는 반지름 $gT_0^2/\pi^2$인 원을 일정한 높이의 수평선 $y=2gT_0^2/\pi^2$에 접하게 굴릴 때 원점에서 바닥과 접촉했던 점이 그리는 곡선이고, $\theta$는 원의 중심과 이 점을 잇는 선분이 수직과 이루는 각을 나타낸다. 

위에서 구한 cycloid 곡선을 도착시간 공식에 대입해서 확인해 보자. $h-y= \frac{gT_0^2}{\pi^2} (\cos \theta - \cos \theta_0)$이고,

$$ d\ell = \frac{gT_0^2 }{\pi^2}\sqrt{2(1+\cos \theta) } d \theta $$

이므로 내려가는데 걸리는 시간 \begin{align} T(h) & = \frac{T_0}{\pi} \int_0^{\theta_0} \sqrt{ \frac{1+\cos \theta}{ \cos \theta - \cos \theta_0 }} d \theta \\ &= \frac{2T_0}{\pi} \int_0^{\theta_0} {\frac{d\sin (\theta/2)}{\sqrt{\sin^2(\theta_0/2)-\sin^2(\theta/2)}}}= T_0 \end{align}이 출발 높이($=h$)에 상관없이 일정함을 확인할 수 있다. 바닥까지 내려가는데 걸리는 시간 $T_0$가 정해지면 원의 반지름 $gT_0^2/\pi$이 결정되어 곡선 모양이 자동으로 정해진다.

https://youtu.be/Ib1TdgeYL4o

Cycloid는 이 성질 이외에도 일정한 중력하에서 두 지점을  연결하는 곡선을 움직일 때 최단 시간을 주는 곡선이기도 하다(brachistochrone curve) 

https://kipl.tistory.com/186

$(1,1)$에서 $(0,0)$까지를 연결하는 일차 곡선 ($y=x$), 이차 곡선 ($y=x^2$), 6차 곡선 ($y=x^6$), 사분원 ($y=1-\sqrt{1-x^2}$) 그리고 cycloid ($x=1-R(\theta-\sin\theta), y=1-R(1-\cos\theta)$) 위를 움직이는 물체의 운동을 mathematica를 사용해서 animation으로 표현하는 방법을 알아보자. 중력가속도는 $g=1$로 놓는다. 적절한 generalized coordinate를 선택해서 Euler-Lagrange equation을 이용하면 운동방정식을 쉽게 구할 수 있다.

(A)  곡선이 $y=f(x)$의 형태로 주어지는 경우 운동방정식은

$$\big[ 1+ (f')^2 \big] \ddot{x} + f' f''  \dot{x} ^2 + f'= 0 .$$

직선경로를 제외하면 운동방정식은 비선형이므로 mathematica의 $\tt NDSolve[]$을 이용해서 수치적으로 푼다.

(B) 원의 경우는 $x$ 좌표보다는 각변수를 이용하면 apparent singularity를 피할 수 있다. 이 경우 운동방정식은

$$ \ddot{\theta} = -\sin \theta,$$

로 주어진다. 

(C) cycloid는 곡선을 따라 움직이는 시간

$$t =\int \frac{ds}{v} = \int  \sqrt{\frac{1 + (dx/dy)^2}{2g(1-y)}}dy$$

을 최소로 만들어주는 곡선이다. cycloid는 다음과 같이 $R$ 변수와 각도 변수 $\theta$로 표현할 수 있다.

$$ 1-x=R(\theta-\sin \theta),~~y-1= -R(1-\cos \theta)$$

이 곡선이 $(0,0)$을 지나야 하는 조건에서 $R$과 그 때의 $\theta$ 값을 구할 수 있다. 먼저 $\theta$을 소거하면,

$$ R \cos \Big( \frac{1+\sqrt{2R-1}}{R} \Big) + 1 = R $$

을 얻고, 이 식의 근을 구하면 $R$ 값이 정해진다. 또한, $$1=R(\theta- \sin \theta)$$을 풀어서 $(0,0)$에 도달할 때 $\theta=\theta_0$ 값을 얻을 수 있다. 그리고 시간과 $\theta$ 변수의 관계는 위의 표현을 적분에 대입하면 

$$t = \sqrt{ \frac{R}{g} }  \theta $$

로 주어짐을 알 수 있다. 이는 사이클로이드가 일정하게 굴러가는 바퀴의 한 점이 그리는 자취이기 때문이다.

아래는 5가지 경우의 곡선 각각에서 운동을 보여주는 mathematica 코드다. 곡선의 모양에 따라 바닥에 도착하는 시간이 다름을 알 수 있다. 출발 높이가 $H$일 때 걸리는 시간은 $\sqrt{H/g}$ 단위로 

직선: $t_1=\int_0^1{ \frac{dy}{\sqrt{1-y}}} = 2$

2차 곡선: $t_2=\int_0^1\sqrt{ \frac{1+4y}{8y(1-y)}}dy= 1.86336$

6차 곡선: $t_6=\int_0^1 \sqrt{\frac{1+36y^{5/3}}{72y^{5/3}(1-y)}}dy=1.90954$

4분원: $t_c=\int_0^{\pi/2} \frac{d \theta}{\sqrt{2\sin \theta }}=1.85407$

cycloid: $t_0= \sqrt{R}\theta_0 = 1.82568$

단순진자는 원호 위에서 반복운동을 한다. 수직에 대해 벌어진 각이 $\theta$일 때 각에 대한 운동 방정식은

$$ \ddot \theta = - \frac{g}{L} \sin \theta.$$

진폭이 작은 경우 ($|\theta| \ll 1$) 윗 식은 용수철 진자의 운동인 단순 조화 운동이 되고 주기는 진폭에 무관하게 일정한 값을 가지게 된다:

$$ \ddot \theta \approx - \frac{g}{L} \theta    \quad \Leftrightarrow  \quad \ddot{x} = - \omega^2 x.$$

그러나 단순진자의 진폭이 일정 이상 커져 작은 각 근사에서 벗어나면 주기는 진폭에 따라 달라짐이 잘 알려져 있다.

진자가 원호가 아닌 다른 곡선 위를 움직일 때 주기가 진폭에 무관하게 주어질 수 있는지 알아보자. 이 경우는 각보다는 용수철 진자처럼 평형점에서 움직인 거리를 이용해서 운동을 기술하는 것이 더 편리하다. 단순진자의 경우 평형점에서 잰 원호의 거리를 $s$라면 $s=L \theta$로 표현되고 작은 각 근사에서 운동 방정식은 
$$ \ddot {s} =-\omega^2  s.$$

이제 진자가 움직이는 곡선에 어떤 제약이 들어오는지 살펴보자. 먼저 움직인 거리에 대한 운동 방정식은 단순조화운동식과 같아야 하므로 위의 형태는 변하지 않아야 한다. 진자가 움직이는 곡선이 $y(x)$로 표현되면 평형점($x=0$) 에서 움직인 거리($x <0$이면 움직인 거리의 음수)는

$$s = \int_0^x \sqrt{ 1+ \Big(\frac{dy}{dx}\Big)^2} dx$$

로 표현된다. $s$에 대한 단순 조화 진동은 위치 에너지가 $U(s) = \frac{1}{2} m\omega^2 s^2$인 경우에 해당하는데 진자는 중력의 영향을 받으므로 이 위치 에너지는 결국 중력 위치 에너지 표현되어야 한다: 

$$ \frac{1}{2} m\omega^2 s^2 = mgy.$$

양변을 $x$에 대해 미분한 후 정리하면

$$ \frac{dy}{dx} = \sqrt{ \frac{2\omega^2 y}{  g - 2\omega^2 y}}.$$

이 방정식을 풀기 위해서 새로운 매개변수 $\psi$를 도입하는데, $dy/dx$가 접선의 기울기이므로 $dy/dx=\tan (\psi/2)$로 놓으면(각은 나중을 위해서 2배 한 것임), 

$$   \sin^2(\psi/2) = \frac{2\omega^2 }{g} y  \quad \Longrightarrow \quad y = \frac{g}{4\omega^2} (1 - \cos\psi).$$

$dx/d\psi  = (dy/d\psi) / (dy/dx)$을 계산해서 적분하면 ($x(\psi=0)=c$)

$$  \frac{dx}{d\psi} = \frac{g}{4\omega^2} (1+\cos \psi)\quad \Longrightarrow \quad x= \frac{g}{4\omega^2} (c+\psi + \sin \psi).$$

이제 $\psi \rightarrow \pi +\psi, c=-\pi $로 변수 치환을 하면(이 경우 $dy/dx= -\cot(\psi/2)$) 진자가 움직여야 하는 곡선이 우리가 잘 알고 있는 cycloid임을 알 수 있다.

$$\begin{matrix} x= a ( \psi -\sin \psi )  \\ y=a(1 + \cos \psi)\end{matrix} ~~~~\left(a \equiv \frac{g}{ 4\omega^2}\right).$$

이 곡선은 반지름 $a$인 원이 $y=2a$인 수평선을 따라 구를 때, 원이 처음 $y=2a$와 접하는 점이 그리는 자취를 나타내고, $\psi$는 원의 중심과 그 점이 잇는 선분이 수직과 이루는 각이다.

Cycloid 모양을 결정하는 $a$가 정해지면 진자의 각진동수 $\omega=\sqrt{g/4a}$를 알 수 있고 주기는 $$T=\frac{2\pi}{\omega }= 4\pi \sqrt{\frac{a}{g}}$$

로 주어진다. 곡선이 주어졌으므로 처음 $y=h$에서 출발할 때 구체적으로 주기를 확인해 보자. 역학적 에너지가 보존되므로 

\begin{align} E &=\frac{1}{2} m \Big( \frac{ds}{dt}\Big)^2 +\frac{1}{2} m \omega^2 s^2 \\&= \frac{1}{2} \Big( \frac{ds}{dt}\Big)^2 + mgy = mgh\\ \Longrightarrow~~ dt &= \pm \frac{ds}{\sqrt{2g(h-y)}} \end{align} 주기는 $y=h$에서 출발해서 바닥에 도달하는데 걸리는 시간의 4배이므로 \begin{align} T &= 4 \int_0^h \frac{ds}{\sqrt{2g(h-y)}} \\ &= \frac{4}{\sqrt{2g}} \int_{\pi/2}^{\psi_0} \frac{-4a d \cos (\psi/2)}{\sqrt{2a[\cos^2(\psi_0/2) - \cos^2(\psi/2)]}} \\ &=4\pi \sqrt{\frac{a}{g}}\end{align} 즉, 주기는 출발 높이에 무관하게 주기가 일정함을 알 수 있다.

공을 cycloid 모양으로 생긴 골짜기에 굴리면 등시운동을 하지만, 그럼 등시진자는 어떻게 만들수 있을까? 이 문제도 역시 cycloid로 해결이 된다. 위에서 구한 cycloid를 y방향으로 $-2a$ 만큼 평행이동시킨 모양을 고려하자. $$ \begin{matrix} x = a (\psi - \sin \psi) \\ y = a( \cos \psi - 1)\end{matrix}$$이 식으로 표현된 cycloid 모양의 천정을 만든 후(그림의 실선), 원점(꼭대기)에 길이 $L$인 줄을 고정시키고 끝에는 무거운 추를 매단다. 추을 진동을 시키면 줄의 일부는 cycloid 모양의 천정을 따라 접하고 나머지 부분은 직선의 형태로 된다.

줄과 cycloid가 접하는 끝지점을 $(x, y)$라 할 때 접하는 부분의 줄의 길이는 $$ \ell = \int_0^\psi ds = a \int_0^\psi \sqrt{ (1-\cos \psi')^2 + (\sin \psi')^2} d\psi' = 4a [1- \cos (\psi/2)]$$로 주어진다. $(x, y)$ 이후의 줄은 접선의 방향으로 나간다. 접선의 기울기를 $\frac{dy}{dx}=\tan \phi$로 놓으면 $\phi=\psi/2 - \pi/2$이고, 직선 부분의 길이가 $L- \ell$이므로 추의 위치는 $$ \begin{matrix} X = x + (L- \ell)\cos \phi = (L - 4a) \cos \phi + a(\psi + \sin \psi) \\ Y = y+(L-\ell) \sin \phi =(L-4a)\sin \phi - a(3+ \cos \psi)  \end{matrix}$$로 주어진다. 줄의 길이를 $L=4a$로 선택하면 추의 위치 $(X, Y)$도 (평행이동된) cycloid(그림의 점선) 상에서 움직임을 알 수 있다. 따라서 이렇게 만들어진 추의 주기는 등시성을 갖는다. $$ \text{추의 위치:}~~\left\{ \begin{array}{l} X= a (\psi + \sin \psi)  \\ Y = -a( 3 + \cos \psi)\end{array}\right. $$

다시 이 진자의 주기를 구체적으로 확인하면, 

$$ds=  \sqrt{dX^2 + dY^2} = \pm a\sqrt{2(1+\cos \psi)} {d\psi} $$

이고, 역학적 에너지가 보존되므로($\Delta y = a (\cos\psi - \cos \psi_0)$)  

\begin{align} \tau &= 4 \int_{0}^{\psi_0} \frac{ds}{\sqrt{2g \Delta y} }  \\  &= 4\sqrt{\frac{a}{g}} \int_{0}^{\psi_0} \sqrt{\frac{1+\cos \psi}{\cos \psi - \cos\psi_0}} d\psi  \\ &= 4\pi \sqrt{ \frac{a}{g}} = 2\pi \sqrt{ \frac{L}{g}}\end{align}이다. 즉, 줄의 길이가 $L=4a$인 단진자가 작은 진동을 할 때의 주기와 동일하고, cycloid에서 미끄러지면서 운동하는 물체의 진자와도 같음을 알 수 있다.