Geometry & Recognition

Catenary는 여러 가지 놀라운 특징을 가지고 있는데 그중 하나가 포물선을 직선 위에서 굴릴 때 초점이 그리는 자취의 모양도 준다는 점이다. 포물선을 직선 위에서 굴리면 포물선 상의 각 점들은 회전과 동시에 병진 운동을 한다. 포물선의 초점이 어떻게 변화는 보기 위해서 구체적인 포물선을 사용하자. 포물선이 $4a y = x^2$으로 쓰면 초점은 $(0, a)$으로 주어진다. 포물선의 구름을 기술할 때는 매개변수를 사용하는 것이 편리하다. 꼭짓점에 해당하는 매개변수 값을 $t=0$으로 잡으면 포물선의 임의의 점은

$$ (x, y ) = (2a t,  at^2)$$

표현할 수 있다. 굴림에 의해서 포물선 상의 한 점 $(x=2at_1, y=at_1^2)$가 $x$-축 위에 놓이게 되었다고 하자. 이때 회전각은 구르기 전 접선의 기울기에 해당하는 각 $\psi = \tan^{-1}(dy/dx)$ 이다 (그림 참조).

이 과정은 접점 $(x,y)$를 회전축으로 해서 초점의 변위 벡터 $(0,a)^T - (x, y)^T$를(그림의 붉은 화살표)는 시계방향으로 회전시킨 후(왼쪽 녹색 화살표), 원점에서 접점까지의 곡선 길이 $s$만큼 $x$축으로 평행이동시키면 된다(오른쪽 파란색 화살표). 곡선의 길이는 매개변수로 표현하면

$$s= \int_0^{t_1} \sqrt{  (2a)^2 + (2at')^2 } dt' = a(  t_1 \sqrt{1+t_1^2} + \sinh^{-1}(t_1)),$$

이다. 시계방향으로 회전행렬은

$$ \mathbf{R}(\psi) =  \begin{pmatrix} \cos\psi & \sin \psi  \\ -\sin\psi & \cos \psi\end{pmatrix}  ,\quad \tan\psi = \frac{dy}{dx}=\frac{dy/dt}{dx/dt} = t_1 $$

로 표현할 수 있다. 따라서, 이 굴림에 의해서 초점의 위치는

$$ \left(\begin{array}{c} X\\Y\end{array}\right) = \mathbf{R} .\left( \begin{array}{c} 0 - 2at_1 \\ a- at_1^2 \end{array}\right) +   \left( \begin{array}{c} s  \\ 0 \end{array} \right)$$

로 옮긴다. 이를 정리하면 다음 식을 얻는다.

$$ X= a\sinh^{-1}(t_1),\quad Y = a \sqrt{1+t_1^2}$$

이 식에서 $t_1$을 소거하면 초점의 자취가 catenary임을 명확히 볼 수 있다.

$$ Y= a \cosh (X/a)$$

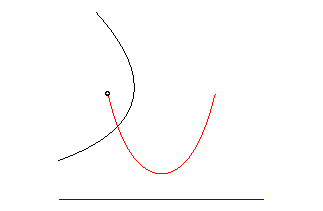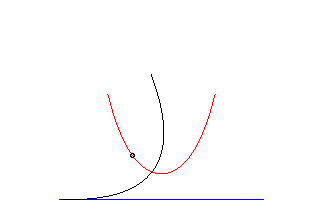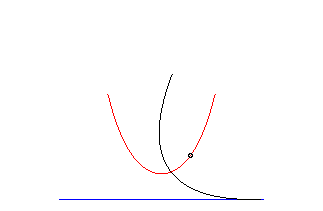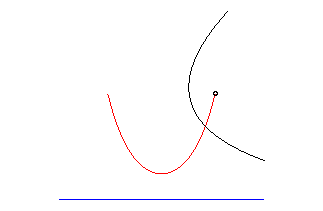
구르는 포물선의 꼭짓점의 자취는 

$$ X=- \frac{at}{\sqrt{1+t^2}} + a\sinh^{-1}(t), \quad Y= \frac{at^2}{\sqrt{1+t^2}}$$

처럼 주어진다. 따라서 초점과 꼭짓점을 알므로 구르는 포물선도 쉽게 그릴 수 있다.

바퀴를 원형으로 만드는 것보다는 네모로 만드는 것이 가공 측면에서 더 쉽다(?). 그러나 네모 바퀴는 중심이 바닥에서 계속 위-아래로 움직이므로 승차감이 떨어진다. 수평 바닥을 움직일 때 무게중심은 바퀴의 대각선이 수직으로 설 때 바닥에서 가장 높고, 한 변이 접할 때 바닥에서 가장 낮으므로, 바퀴 중심이 일정한 높이에서 움직이게 하려면 바닥의 모양을 평평할 수 없다. 바퀴의 무게중심이 출렁거림 없이 움직이기 위해서는 바닥의 모양이 어떤 형태로 주어야 져야 하는지 알아보자.

https://www.youtube.com/watch?v=qFVti39MvX8

우선 바퀴의 한 변의 길이를 $2\ell$로 하자. 그러면 평평한 바닥일 때 무게중심은 바닥에서 최대로 $\sqrt{2}\ell$ 만큼 올라가므로, 바닥을 변형시킬 때 이 높이를 유지할 수 있도록 모양을 선택하고 이때 곡선을 기술하는 $x$ 좌표를 $x=0$으로 잡는다. $x>0$일 때 바퀴의 한 변이 접하는 접점의 좌표를 $(x, y)$라면, 이 점에서 기울기가 $y' =dy/dx =\tan \psi$이므로 접선의 방정식은 ($(X,Y)$로 표현) 

$$Y - y = y' (X - x) $$

로 표현된다. 그리고 바퀴의 중심은 $(x, \sqrt{2}\ell)$에 있음을 알 수 있고, 중심에서 접선에 가장 가까운 점을 $(X_0, Y_0)$라고 하면 그림에서

$$X_0 - x = (\sqrt{2}\ell- y)\sin \psi \cos \psi = (\sqrt{2}\ell- y) \frac{y'}{{1+(y')^2}} ,$$

$$\sqrt{2}\ell - Y_0 = (\sqrt{2}\ell -y) \cos^2 \psi = (\sqrt{2}\ell-y) \frac{1}{{1+ (y')^2}}.$$

임을 알 수 있다. 바퀴 중심에서 접선까지 거리가 $\ell$이므로 이를 두 점 $(x, \sqrt{2}\ell)$, $(X_0, Y_0)$의 사이거리로 표현하면

$$\ell^2  =  (x - X_0)^2 + (\sqrt{2}\ell- Y_0)^2$$

위의 관계를 정리하면

$$ \ell^2 = (\sqrt{2}\ell- y)^2 \left[ \frac{(y')^2}{ (1+ (y')^2)^2}  + \frac{1}{(1+(y')^2 )^2}\right]$$

이므로 곡선에 대한 다음 식을 얻는다.

$$y = \sqrt{2}\ell - \ell \sqrt{1+ (y')^2}$$

한 번 더 미분하면,

$$ y'' = -\frac{1}{\ell} \sqrt{1 + (y')^2}$$

이어서 위로 볼록인 catenary 형태로 바닥이 만들어져야 함을 알 수 있다. 

$y(0)=0$, $y'(0)=1$을 만족해야 하므로 해는

$$ y= \sqrt{2}\ell - \ell \cosh[ \cosh^{-1}(\sqrt{2}) - x/\ell]$$

임을 알 수 있고, 언덕 하나를 넘는 동안 수평이동거리는 $x= 2\ell \cosh^{-1}(\sqrt{2})\approx 1.76275\ell$이다. 중심이 등속운동($dx/dt = v$)을 하는 경우 바퀴의 회전각속도는 ($y'=\tan\psi$)

$$\frac{d\psi}{dt} = v\cos^2(\psi) y'' = -\frac{v}{\sqrt{2}\ell - y}= - \frac{v}{\ell \cosh[\cosh^{-1}(\sqrt{2})- vt/\ell] }$$

이므로 등각속도 운동은 아니다.

Ref: https://my.vanderbilt.edu/stacyfonstad/files/2011/10/squareWheels.pdf