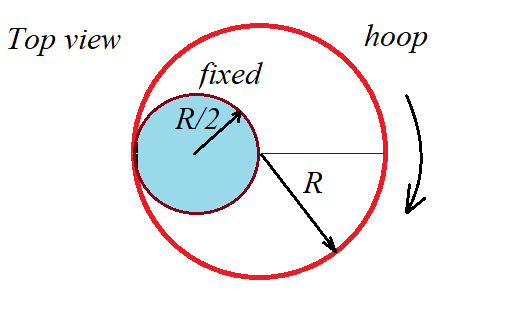
반지름 $R$인 훌라후프가 반지름이 $R/2$인 사람 허리를 축으로 일정하게 돌고 있다. 훌라후프 중심이 돌아가는 각속도가 $\omega$일 때 운동에너지는 어떻게 표현되는가? 후프의 회전관성은 $MR^2$이다.
1. $\frac{5}{8} MR^2 \omega^2$
2. $MR^2\omega^2$
3. 이중에 답이 없다.
훌라후프의 순간적인 회전축은 원기둥의 중심이다.

원기둥의 중심에 대한 회전관성은 $I_{AOIR} = MR^2 + M(R/2)^2=\frac{5}{4}MR^2$이므로
$$ K = \frac{1}{2}I_{AOIR}\omega^2 = \frac{5}{8}MR^2 \omega^2$$
'Physics > 역학' 카테고리의 다른 글
| 반구체의 질량중심은? (0) | 2022.02.14 |
|---|---|
| 얼마나 일을 해야 하는가? (0) | 2022.02.11 |
| 얼마나 회전한 것인가? (0) | 2022.02.11 |
| 물체가 맨 아래에 내려왔을 때 장력은? (0) | 2022.02.10 |
| 배가 이동한 거리는? (0) | 2022.02.10 |







